This is an Excel replica of excellent Tableau visual made by Marc Reid here.
Last week, I saw a stunning visualization on Tour de France using of radial charts on twitter.
???? @Marc_DS5 combined #SportsVizSunday (Tour de France) and #SWDChallenge (radial charts) to create this #VOTD! Learn about the fastest and longest tours in history: https://t.co/Xge6mtyVYE pic.twitter.com/6luDs9Riwp
— Tableau Public (@tableaupublic) July 9, 2019
As an amateur cyclist, somewhat pro data analyst, I jumped with joy seeing that visual. I immediately thought, this needs to be redone in Excel. So here is an implementation of radial charts in Excel.
Demo of Excel Replica – TdF Distance & Pace Radial charts

Download Tour de France Radial Charts viz in Excel
Click here to download the completed workbook. Have a play with the viz tab or explore the data&calc tab to see how it’s put together.
How is this chart made?
This will be a brief recipe with links to other articles that explain the technical elements. Feel free to poke around the download file to discover odd missing elements.
Step 0: Inspiration
As mentioned earlier, the inspiration for this came from Marc Reid’s excellent visual. I loved the visual instantly and wanted to replicate it in Excel as much as possible.

Step 1: Getting data
The data for this came from Thomas Camminady’s page on Every cyclist of Tour de France in a single CSV file. As the name suggests, it’s a CSV file, so there was no post processing needed. For each year, each finisher there is one row in the data set with columns like name, team name, duration, distance, pace, position and few other bits.
Step 2: Calcs for radial visualization
Meet ometrys. You might have seen them back in high school.
- Geometry
- Trigonometry
They will help us take the cycling data and transform that in to a radial chart.
Since there is 94 years of data (between 1913 and 2017 there were 94 editions of the tour) each spoke will be separated by 2pi / 94 radians.
Let’s take a look the anatomy of radial chart spokes.


We could simply draw one line per spoke, but to get the thick edge, thin center look, I went with triangle approach.
As you can see, if we can calculate points a,b,c & d for each year, our job is done.
The center is (0,0). Points a & d lie on the inner ring. Points b & c depend on the actual distance (or pace) we are plotting for the given year.
Let’s say inner ring size (radius) is defined by a named range hole.size and triangle edges are separated by 1 degree (2pi/360 radians).
- point a (x,y) = (hole.size * SIN(theta), hole.size *COS(theta))
- point d (x,y) = (hole.size * SIN(theta + 2pi/360), hole.size *COS(theta + 2pi/360))
To calculate b & c, we need to use the distance in that year too. As the distances (and paces) are all over the places, I have used a scale.factor to scale them down or up to make the radial charts uniform. This is how the formula looks for points b & c.
- point b (x,y) = (dist/scale.factor.d * SIN(theta), dist/scale.factor.d * COS(theta))
- point c (x,y) = (dist/scale.factor.d * SIN(theta + 2pi/360), dist/scale.factor.d * COS(theta + 2pi/260))
As we need 4 points for each year, we need to calculate 4 x 94 values to plot the radial chart for distance. Similar set of values need to be calculated for pace too.
Once all these values are ready, it is a simple matter of creating XY scatter plot, formatting it to get the spokes.
This method of drawing spokes / radials in Excel is explained in great detail here. For more also see network relationships chart in Excel.
The calculations for line charts are rather straight forward, so I am not explaining them here.
Step 3: Extra series for highlighting max, min and selected values
Once the calculations are done, we can add additional x,y values for each of these scenarios.
- If the pace is maximum, then get (x,y) else (NA(), NA())
- Pace is minimum, get (x,y) else NA()
- Year is selected by the user, get (x,y) else NA()
Related: How to conditionally format charts?
Step 4: User interaction for year selection – scrollbar form control
I added a scrollbar control to the visuals area and then set it up to go from 1913 to 2017. We can use the linked cell value to drive the calculations needed for “year selection” bit.

Related: Introduction to Excel Form Controls
Step 5: Stats for selected year with Picture Link
For the selected year, we can easily calculate stats (winner’s name, duration, distance, pace and percentage changes compared to previous edition of the tour). Once these stats are calculated, we can show them on the visual by using picture link. As you play with the scrollbar, the picture link changes.
Here is a re-cap of all the 5 steps in construction.

Other bits & pieces
- We can add labels for important points on radial chart by using “value from cell” option for data labels.
- But the labels on XY charts tend to be poorly positioned. I needed more space between edge of spoke and label. To get this, I added an extra label series that is offset 12 points from the edge.
- We can add number of finishers in each year and see that trend too. As you can see, over the years, the competition has gone intense.
The final output – Tour de France distance & pace over time as radial charts

How do you like the visualization?
My love for cycling, data and story-telling coincided perfectly in this. That said, if I remove my rose-tinted glasses, I can see a couple of issues with the visualization.
- Redundancy: The line charts at bottom depict the same info as radials, but do a better job. They can work even with 500 data points, where as the radial spokes will get very busy with such large volume of data.
- Obvious: The conclusion from visualization is “as distance goes down, pace has gone up”. But this is kind of obvious.
That said, I loved the challenge of replicating it in Excel. I would say, barring the trigonometry part, it is rather simple to re-create this in Excel. I suggest giving it a try to improve your charting skills.
What about you? What do you think about the original Tableau visual and its replica in Excel? Please share your thoughts in comment section.
Do you like sport & data – Check out these stories too:
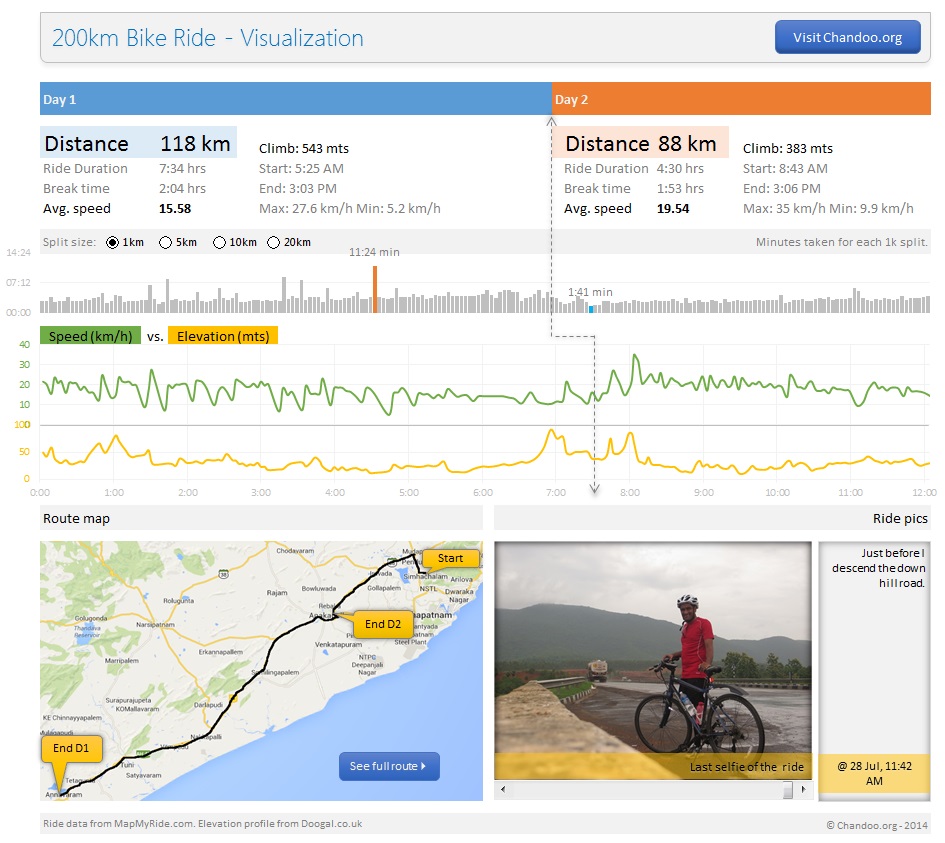
My first 200km bike ride as a dashboard
Roger Federer’s 7th Wimbledon Title – Timeline

Commonwealth Games 2018 – Medal Tally Report (Power BI)



















20 Responses to “Simulating Dice throws – the correct way to do it in excel”
You have an interesting point, but the bell curve theory is nonsense. Certainly it is not what you would want, even if it were true.
Alpha Bravo - Although not a distribution curve in the strict sense, is does reflect the actual results of throwing two physical dice.
And reflects the following . .
There is 1 way of throwing a total of 2
There are 2 ways of throwing a total of 3
There are 3 ways of throwing a total of 4
There are 4 ways of throwing a total of 5
There are 5 ways of throwing a total of 6
There are 6 ways of throwing a total of 7
There are 5 ways of throwing a total of 8
There are 4 ways of throwing a total of 9
There are 3 ways of throwing a total of 10
There are 2 ways of throwing a total of 11
There is 1 way of throwing a total of 12
@alpha bravo ... welcome... 🙂
either your comment or your dice is loaded 😉
I am afraid the distribution shown in the right graph is what you get when you throw a pair of dice in real world. As Karl already explained, it is not random behavior you see when you try to combine 2 random events (individual dice throws), but more of order due to how things work.
@Karl, thanks 🙂
When simulating a coin toss, the ROUND function you used is appropriate. However, your die simulation formula should use INT instead of ROUND:
=INT(RAND()*6)+1
Otherwise, the rounding causes half of each number's predictions to be applied to the next higher number. Also, you'd get a count for 7, which isn't possible in a die.
To illustrate, I set up 1200 trials of each formula in a worksheet and counted the results. The image here shows the table and a histogram of results:
http://peltiertech.com/WordPress/wp-content/img200808/RandonDieTrials.png
@Jon: thanks for pointing this out. You are absolutely right. INT() is what I should I have used instead of ROUND() as it reduces the possibility of having either 1 or 6 by almost half that of having other numbers.
this is such a good thing to learn, helps me a lot in my future simulations.
Btw, the actual graphs I have shown were plotted based on randbetween() and not from rand()*6, so they still hold good.
Updating the post to include your comments as it helps everyone to know this.
By the way, the distribution is not a Gaussian distribution, as Karl points out. However, when you add the simulations of many dice together (i.e., ten throws), the overall results will approximate a Gaussian distribution. If my feeble memory serves me, this is the Central Limit Theorem.
@Jon, that is right, you have to nearly throw infinite number of dice and add their face counts to get a perfect bell curve or Gaussian distribution, but as the central limit theorem suggests, our curve should roughly look like a bell curve... 🙂
[...] posts on games & excel that you may enjoy: Simulating Dice throws in Excel Generate and Print Bingo / Housie tickets using this excel Understanding Monopoly Board [...]
[...] Correct way to simulate dice throws in excel [...]
[...] Simulate dice throws in excel [...]
I'm afraid to say that this is a badly stated and ambiguous post, which is likely to cause errors and misunderstanding.
Aside from the initial use of round() instead of int(),.. (you've since corrected), you made several crucial mistakes by not accurately and unambiguously stating the details.
Firstly, you said:
"this little function generates a random fraction between 0 and 1"
Correctly stated this should be:
"this little function generates a random fraction F where 0 <= F < 1".
Secondly, I guess because you were a little fuzzy about the exact range of values returned by rand(), you have then been just as ambiguous in stating:
"I usually write int(rand()*12)+1 if I need a random number between 0 to 12".
(that implies 13 integers, not 12)
Your formula, does not return 13 integers between 0 to 12.
It returns 12 integers between 1 and 12 (inclusive).
-- As rand() returns a random fraction F where 0 <= F < 1, you can obviously can only get integers between 1 and 12 (inclusive) from your formula as stated above, but clearly not zero.
If you had said either:
"I usually write int(rand()*12) if I need a random number between 0 to 11 (inclusive)",
or:
"I usually write int(rand()*12)+1 if I need a random number between 1 to 12 (inclusive)"
then you would have been correct.
Unfortunately, you FAIL! -- repeat 5th grade please!
Your Fifth Grade Maths Teacher
Idk if I'm on the right forum for this or how soon one can reply, but I'm working on a test using Excel and I have a table set up to get all my answers from BUT I need to generate 10,000 answers from this one table. Every time, I try to do this I get 10,000 duplicate answers. I know there has to be some simple command I have left out or not used at all, any help would be extremely helpful! (And I already have the dice figured out lol)
Roll 4Dice with 20Sides (4D20) if the total < 20 add the sum of a rerolled 2D20. What is the average total over 10,000 turns? (Short and sweet)
Like I said when I try to simulate 10,000turns I just get "67" 10,000times -_- help please! 😀
@Justin
This is a good example to use for basic simulation
have a look at the file I have posted at:
https://rapidshare.com/files/1257689536/4_Dice.xlsx
It uses a variable size dice which you set
Has 4 Dice
Throws them 10,000 times
If Total per roll < 20 uses the sum of 2 extra dice Adds up the scores Averages the results You can read more about how it was constructed by reading this post: http://chandoo.org/wp/2010/05/06/data-tables-monte-carlo-simulations-in-excel-a-comprehensive-guide/
Oh derp, i fell for this trap too, thinking i was makeing a good dice roll simulation.. instead of just got an average of everything 😛
Noteably This dice trow simulate page is kinda important, as most roleplay dice games were hard.. i mean, a crit failure or crit hit (rolling double 1's or double 6's) in a a game for example dungeons and dragons, if you dont do the roll each induvidual dice, then theres a higher chance of scoreing a crit hit or a crit failure on attacking..
I've been working on this for awhile. So here's a few issues I've come across and solved.
#1. round() does work, but you add 0.5 as the constant, not 1.
trunc() and int() give you the same distributions as round() when you use the constant 1, so among the three functions they are all equally fair as long as you remember what you're doing when you use one rather than the other. I've proven it with a rough mathematical proof -- I say rough only because I'm not a proper mathematician.
In short, depending on the function (s is the number of sides, and R stands in for RAND() ):
round(f), where f = sR + 0.5
trunc(f), where f = sR + 1
int(f), where f = sR + 1
will all give you the same distribution, meaning that between the three functions they are fair and none favors something more than the others. However...
#2. None of the above gets you around the uneven distribution of possible outcomes of primes not found in the factorization of the base being used (base-10, since we're using decimal; and the prime factorization of 10 is 2 and 5).
With a 10-sided die, where your equation would be
=ROUND(6*RAND()+0.5)
Your distribution of possible values is even across all ten possibilities.
However, if you use the most basic die, a 6-sided die, the distributions favor some rolls over others. Let's assume your random number can only generate down to the thousandths (0.000 ? R ? 0.999). The distribution of possible outcomes of your function are:
1: 167
2: 167
3: 166
4: 167
5: 167
6: 166
So 4 and 6 are always under-represented in the distribution by 1 less than their compatriots. This is true no matter how many decimals you allow, though the distribution gets closer and closer to equal the further towards infinite decimal places you go.
This carries over to all die whose numbers of sides do not factor down to a prime factorization of some exponential values of 2 and 5.
So, then, how can we fix this one, tiny issue in a practical manner that doesn't make our heads hurt or put unnecessary strain on the computer?
Real quick addendum to the above:
Obviously when I put the equation after the example of the 10-sided die, I meant to put a 10*RAND() instead of a 6*RAND(). Oops!
Also, where I have 0.000 ? R ? 0.999, the ?'s are supposed to be less-than-or-equal-to signs but the comments didn't like that. Oh well.
How do you keep adding up the total? I would like to have a cell which keeps adding up the total sum of the two dices, even after a new number is generated in the cells when you refresh or generate new numbers.
So, how do you simulate rolling 12 dice? Do you write int(rand()*6) 12 times?
Is there a simpler way of simulating n dice in Excel?
I've run this code in VBA
Sub generate()
Application.ScreenUpdating = False
Application.Calculation = False
Dim app, i As Long
Set app = Application.WorksheetFunction
For i = 3 To 10002
Cells(i, 3).Value = i - 2
Cells(i, 4).Value = app.RandBetween(2, 12)
Cells(i, 5).Value = app.RandBetween(1, 6) + app.RandBetween(1, 6)
Next
Application.ScreenUpdating = True
Application.Calculation = True
End Sub
But I get the same distribution for both columns 4 and 5
Why ?
@Mohammed
I would expect to get the same distribution as you have effectively used the same function