When comparing 2 sets of data, one question we always ask is,
- How is first set of numbers different from second set?
A classic example of this is, lets say you are comparing productivity figures of your company with industry averages. Merely seeing both your series as lines (or columns etc.) is not going to tell you the full story. But if we can shade our productivity line in red or green when it is under or above industry average… now that would be awesome! Something like below:
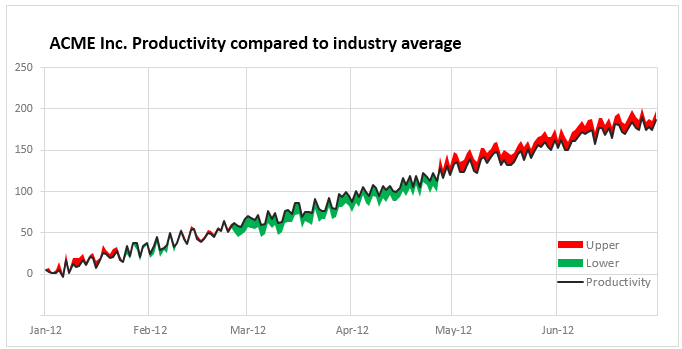
The above chart tells us where we are lagging and where we are good. It will let us ask poking questions about the gap and find answers (may be removing coffee machine from 2nd floor last May was a bad idea!)
So how do we create such a chart?
PS: This chart and article is inspired from a question asked by arobbins & excellent solution provided by Hui here.
Creating a shaded line chart in Excel – step by step tutorial
1. Place your data in Excel
Lay out your data like this.
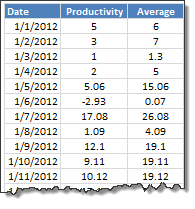
2. Add 3 extra columns – min, lower, upper
If you look at the chart closely, you will realize it is a collection of 4 sets of data. See this illustration to understand.
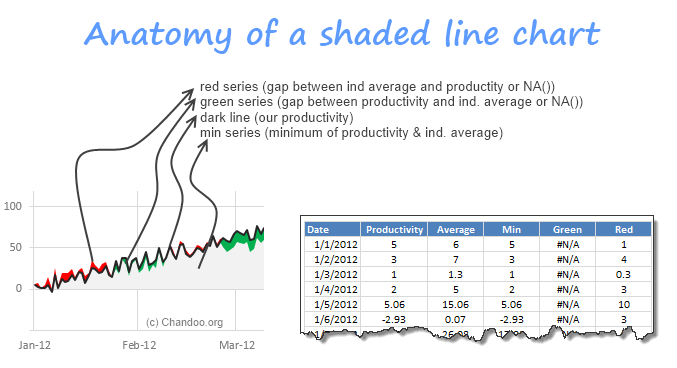
Write formulas to load values in to min, lower (green) & upper (red) series.
- Min is minimum of productivity and ind. average
- Lower (green) is difference between productivity and ind. average (or NA() if negative)
- Upper (red) is difference between ind. average and productivity (or NA() if negative)
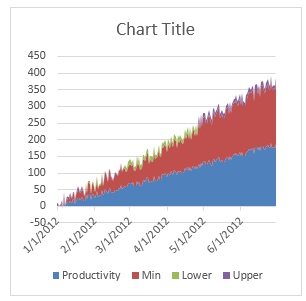
3. Create a stacked area chart from this data
Select all the 4 series (productivity, min, lower & upper) and create a stacked area chart.
This is how it looks.
4. Format the productivity series as line
Right click on productivity series and using “Change series chart type” option, change it to line chart.
5. Make the min series transparent
Select min series and fill it with “No color”
6. Format lower & upper in green & red colors respectively
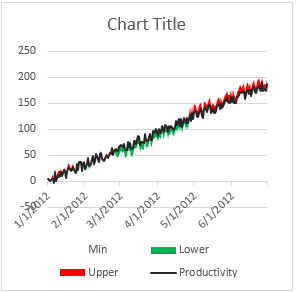
And you are done!
Optional: adjust series formatting, add grid lines etc.
As a bonus, you can add vertical grid lines (so that we can understand the red green changes easily) and format the horizontal axis. You can also move around the legend and remove the words “min” from it.
This will make the chart look really awesome.
Is this the only way to compare productivity with industry averages?
Although our shaded line chart is an excellent way to visualize differences between 2 series of data, I kept thinking if there are other ways to compare this.
After a bit of doodling & drawing inspiration from various charts I have seen earlier, here are 4 more options we can consider.
Option 1 – Productivity vs. variance wrt Ind. average
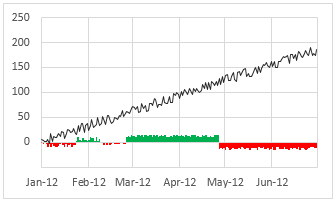
This chart shows the variance (industry average-productity) at bottom so that we can easily look at overall trend & understand how we fared with respect to industry.
To create this chart, you just have to calculate the variance in a separate column and create a column & line chart combination (column for variance & line for productivity). Once such a chart is ready, go to fill options for the column chart and check invert colors if negative option and set up green & red colors!
Option 2 – Productivity vs. better or worse indicators
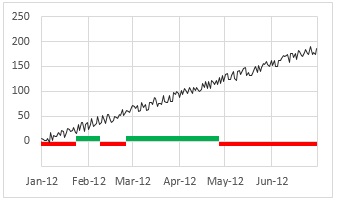
This chart just shows whether productivity surpassed industry average or not in a boolean state (green for yes, red for no)
This chart is a combination of line & column chart with same principle as above (invert if negative option).
Option 2 (made using Excel 2010 Sparklines)
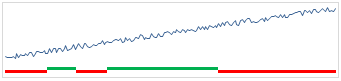
You can create this chart very easily with Excel 2010 sparklines. Line chart for productivity and win-loss chart for better or worse indicators.
Option 3 – Collapsed Productivity vs. variance wrt Ind. average
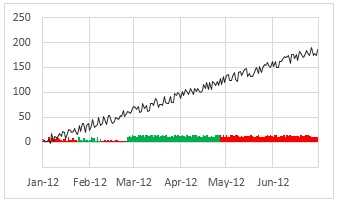
Since the color is already telling us whether variance is negative or positive, we can collapse both to same side of axis (thus saving some space & reducing redundant information).
To create this chart, we need two series of data – positive variance & negative variance as 2 sets of areas on the chart.
Option 4 – Collapsed Productivity vs. better or worse indicators
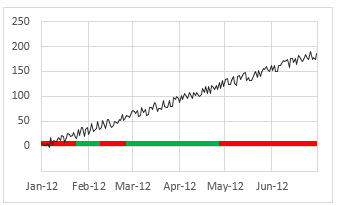
Well, this is same as option 2 but collapsed.
Download Example workbook
Click here to download the Excel workbook containing all these examples. You can also see detailed steps for making the shaded line chart in it.
How do you compare one series with another?
I must confess that I never made shaded line chart until today. For smaller data sets (<15 items), I usually compare by making column charts or thermo-meter charts. These are easy to make and easy to understand. For larger data sets, I try to make dynamic charts so that I can choose which series to include in comparison or make indexed charts.
Now that I learned how to set up shaded line charts, I will try them in my upcoming projects & consulting assignments to see how they fare.
What about you? Which types of charts do you use to compare one series with another? Please share your techniques & implementations using comments. I would love to learn more from you.
Compare often? Check out these charts
If you compare apples to apples (or to an occasional bushel of oranges) for living, then check out these charting tutorials & techniques.
WARNING: After learning these techniques, Suddenly you will become incomparably awesome in your office.
20 Responses to “Simulating Dice throws – the correct way to do it in excel”
You have an interesting point, but the bell curve theory is nonsense. Certainly it is not what you would want, even if it were true.
Alpha Bravo - Although not a distribution curve in the strict sense, is does reflect the actual results of throwing two physical dice.
And reflects the following . .
There is 1 way of throwing a total of 2
There are 2 ways of throwing a total of 3
There are 3 ways of throwing a total of 4
There are 4 ways of throwing a total of 5
There are 5 ways of throwing a total of 6
There are 6 ways of throwing a total of 7
There are 5 ways of throwing a total of 8
There are 4 ways of throwing a total of 9
There are 3 ways of throwing a total of 10
There are 2 ways of throwing a total of 11
There is 1 way of throwing a total of 12
@alpha bravo ... welcome... 🙂
either your comment or your dice is loaded 😉
I am afraid the distribution shown in the right graph is what you get when you throw a pair of dice in real world. As Karl already explained, it is not random behavior you see when you try to combine 2 random events (individual dice throws), but more of order due to how things work.
@Karl, thanks 🙂
When simulating a coin toss, the ROUND function you used is appropriate. However, your die simulation formula should use INT instead of ROUND:
=INT(RAND()*6)+1
Otherwise, the rounding causes half of each number's predictions to be applied to the next higher number. Also, you'd get a count for 7, which isn't possible in a die.
To illustrate, I set up 1200 trials of each formula in a worksheet and counted the results. The image here shows the table and a histogram of results:
http://peltiertech.com/WordPress/wp-content/img200808/RandonDieTrials.png
@Jon: thanks for pointing this out. You are absolutely right. INT() is what I should I have used instead of ROUND() as it reduces the possibility of having either 1 or 6 by almost half that of having other numbers.
this is such a good thing to learn, helps me a lot in my future simulations.
Btw, the actual graphs I have shown were plotted based on randbetween() and not from rand()*6, so they still hold good.
Updating the post to include your comments as it helps everyone to know this.
By the way, the distribution is not a Gaussian distribution, as Karl points out. However, when you add the simulations of many dice together (i.e., ten throws), the overall results will approximate a Gaussian distribution. If my feeble memory serves me, this is the Central Limit Theorem.
@Jon, that is right, you have to nearly throw infinite number of dice and add their face counts to get a perfect bell curve or Gaussian distribution, but as the central limit theorem suggests, our curve should roughly look like a bell curve... 🙂
[...] posts on games & excel that you may enjoy: Simulating Dice throws in Excel Generate and Print Bingo / Housie tickets using this excel Understanding Monopoly Board [...]
[...] Correct way to simulate dice throws in excel [...]
[...] Simulate dice throws in excel [...]
I'm afraid to say that this is a badly stated and ambiguous post, which is likely to cause errors and misunderstanding.
Aside from the initial use of round() instead of int(),.. (you've since corrected), you made several crucial mistakes by not accurately and unambiguously stating the details.
Firstly, you said:
"this little function generates a random fraction between 0 and 1"
Correctly stated this should be:
"this little function generates a random fraction F where 0 <= F < 1".
Secondly, I guess because you were a little fuzzy about the exact range of values returned by rand(), you have then been just as ambiguous in stating:
"I usually write int(rand()*12)+1 if I need a random number between 0 to 12".
(that implies 13 integers, not 12)
Your formula, does not return 13 integers between 0 to 12.
It returns 12 integers between 1 and 12 (inclusive).
-- As rand() returns a random fraction F where 0 <= F < 1, you can obviously can only get integers between 1 and 12 (inclusive) from your formula as stated above, but clearly not zero.
If you had said either:
"I usually write int(rand()*12) if I need a random number between 0 to 11 (inclusive)",
or:
"I usually write int(rand()*12)+1 if I need a random number between 1 to 12 (inclusive)"
then you would have been correct.
Unfortunately, you FAIL! -- repeat 5th grade please!
Your Fifth Grade Maths Teacher
Idk if I'm on the right forum for this or how soon one can reply, but I'm working on a test using Excel and I have a table set up to get all my answers from BUT I need to generate 10,000 answers from this one table. Every time, I try to do this I get 10,000 duplicate answers. I know there has to be some simple command I have left out or not used at all, any help would be extremely helpful! (And I already have the dice figured out lol)
Roll 4Dice with 20Sides (4D20) if the total < 20 add the sum of a rerolled 2D20. What is the average total over 10,000 turns? (Short and sweet)
Like I said when I try to simulate 10,000turns I just get "67" 10,000times -_- help please! 😀
@Justin
This is a good example to use for basic simulation
have a look at the file I have posted at:
https://rapidshare.com/files/1257689536/4_Dice.xlsx
It uses a variable size dice which you set
Has 4 Dice
Throws them 10,000 times
If Total per roll < 20 uses the sum of 2 extra dice Adds up the scores Averages the results You can read more about how it was constructed by reading this post: http://chandoo.org/wp/2010/05/06/data-tables-monte-carlo-simulations-in-excel-a-comprehensive-guide/
Oh derp, i fell for this trap too, thinking i was makeing a good dice roll simulation.. instead of just got an average of everything 😛
Noteably This dice trow simulate page is kinda important, as most roleplay dice games were hard.. i mean, a crit failure or crit hit (rolling double 1's or double 6's) in a a game for example dungeons and dragons, if you dont do the roll each induvidual dice, then theres a higher chance of scoreing a crit hit or a crit failure on attacking..
I've been working on this for awhile. So here's a few issues I've come across and solved.
#1. round() does work, but you add 0.5 as the constant, not 1.
trunc() and int() give you the same distributions as round() when you use the constant 1, so among the three functions they are all equally fair as long as you remember what you're doing when you use one rather than the other. I've proven it with a rough mathematical proof -- I say rough only because I'm not a proper mathematician.
In short, depending on the function (s is the number of sides, and R stands in for RAND() ):
round(f), where f = sR + 0.5
trunc(f), where f = sR + 1
int(f), where f = sR + 1
will all give you the same distribution, meaning that between the three functions they are fair and none favors something more than the others. However...
#2. None of the above gets you around the uneven distribution of possible outcomes of primes not found in the factorization of the base being used (base-10, since we're using decimal; and the prime factorization of 10 is 2 and 5).
With a 10-sided die, where your equation would be
=ROUND(6*RAND()+0.5)
Your distribution of possible values is even across all ten possibilities.
However, if you use the most basic die, a 6-sided die, the distributions favor some rolls over others. Let's assume your random number can only generate down to the thousandths (0.000 ? R ? 0.999). The distribution of possible outcomes of your function are:
1: 167
2: 167
3: 166
4: 167
5: 167
6: 166
So 4 and 6 are always under-represented in the distribution by 1 less than their compatriots. This is true no matter how many decimals you allow, though the distribution gets closer and closer to equal the further towards infinite decimal places you go.
This carries over to all die whose numbers of sides do not factor down to a prime factorization of some exponential values of 2 and 5.
So, then, how can we fix this one, tiny issue in a practical manner that doesn't make our heads hurt or put unnecessary strain on the computer?
Real quick addendum to the above:
Obviously when I put the equation after the example of the 10-sided die, I meant to put a 10*RAND() instead of a 6*RAND(). Oops!
Also, where I have 0.000 ? R ? 0.999, the ?'s are supposed to be less-than-or-equal-to signs but the comments didn't like that. Oh well.
How do you keep adding up the total? I would like to have a cell which keeps adding up the total sum of the two dices, even after a new number is generated in the cells when you refresh or generate new numbers.
So, how do you simulate rolling 12 dice? Do you write int(rand()*6) 12 times?
Is there a simpler way of simulating n dice in Excel?
I've run this code in VBA
Sub generate()
Application.ScreenUpdating = False
Application.Calculation = False
Dim app, i As Long
Set app = Application.WorksheetFunction
For i = 3 To 10002
Cells(i, 3).Value = i - 2
Cells(i, 4).Value = app.RandBetween(2, 12)
Cells(i, 5).Value = app.RandBetween(1, 6) + app.RandBetween(1, 6)
Next
Application.ScreenUpdating = True
Application.Calculation = True
End Sub
But I get the same distribution for both columns 4 and 5
Why ?
@Mohammed
I would expect to get the same distribution as you have effectively used the same function