Whenever we deal with large amounts of data, one of the goals for analysis is,
How is this data distributed?
This is where a Box plot can help. According to Wikipedia, a box plot is a convenient way of graphically depicting groups of numerical data through their five-number summaries: the smallest observation (sample minimum), lower quartile (Q1), median (Q2), upper quartile (Q3), and largest observation (sample maximum) [more]
Quartile?!? What is that like?
When we say $ 39,000 is the lower quartile of salaries paid in Acme inc. it means, 25% of people make less than or equal to $39,000
Like that Median (Q2) means half the samples are lower than median & the other are more than median.
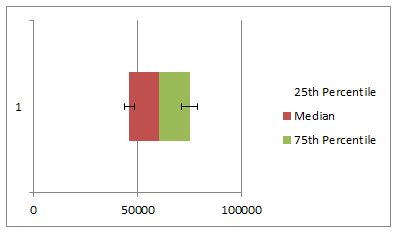
Example Box Plot
Here is an example box plot depicting salaries of all analysts in USA as per our recent Excel Salary Survey.
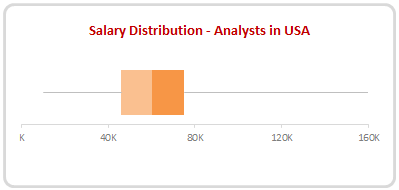
The box shows distribution of middle half of data (salaries) while the lines (called as whiskers) show minimum and maximum salaries.
As you can see, 50% of the analysts make between $46,000 to $75,000 while the min is $10k and max is $160k.
Why use Box plots?
Box & whisker plots are an excellent way to show distribution of your data without plotting all the values. They are easy to understand. We can use them whenever we have lots of data or dealing with samples drawn from larger population.
Creating Box plots in Excel – 9 step tutorial
Despite their utility, Excel has no built-in option to make a box plot. Of course you can make a 3D pie chart or stacked horizontal pyramid chart. Lets save them for your last day at work and understand how to create box plots in Excel.
Step 1: Calculate the number summaries
Assuming your data is in list use formulas MIN, MAX & PERCENTILE to calculate summaries like below:
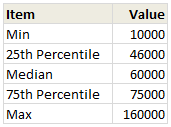
To calculate 25th percentile (Q1) use = PERCENTILE(list, 25%)
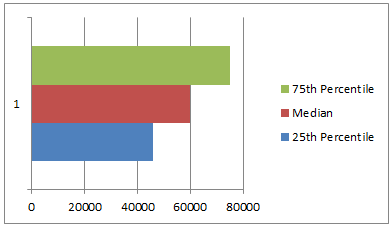
Step 2: Make a bar chart from Q1, Median & Q3
Just select the 25th percentile, median & 75th percentile values and create a bar chart.Make sure that your chart shows 3 different colored bars not 3 bars in one color.
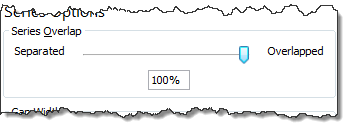
Step 3: Set series overlap to 100%
Select any bar, press CTRL+1 (right click > format series) and adjust series overlap to 100%
Step 4: Adjust series order so that you can see all the bars
If you cannot see all the bars, right click on chart, click on “Select data”.
Now, adjust the series order using arrow keys so that you can see all the bars. See this demo:
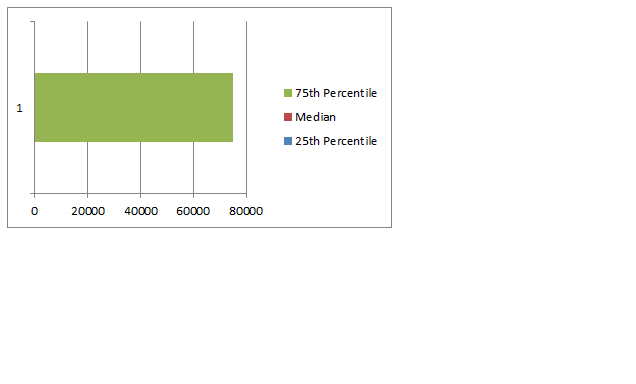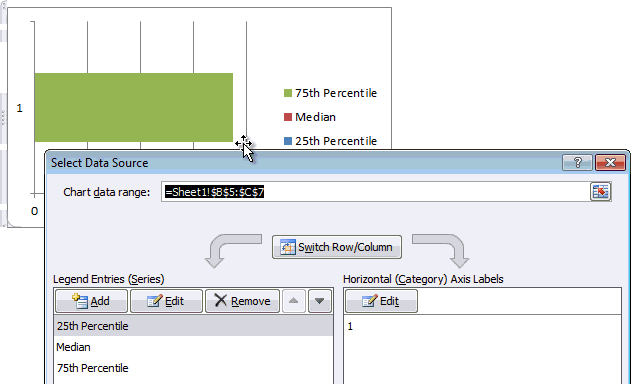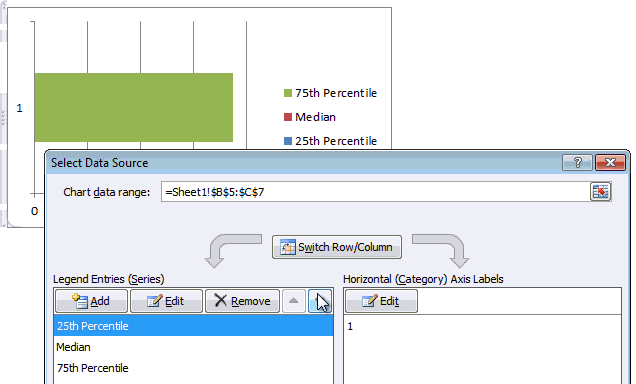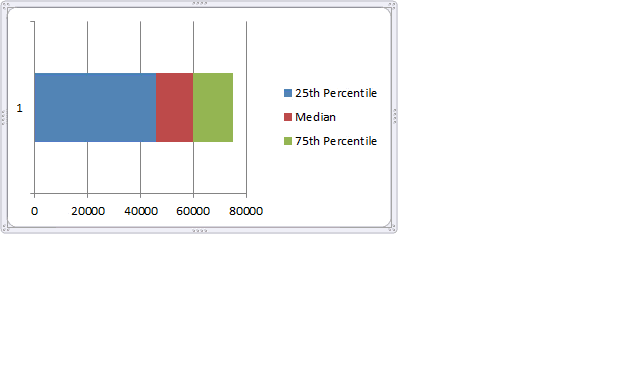
Step 5: Make 25th percentile (Q1) bar invisible
Select the bar corresponding to Q1 and fill it with white color. If you make it transparent, it will not work. So make it all white.
Step 6: Add error bars to Q1 & Q3 series
Just select Q1 (25th percentile) bar and add error bar (any type) from layout ribbon.
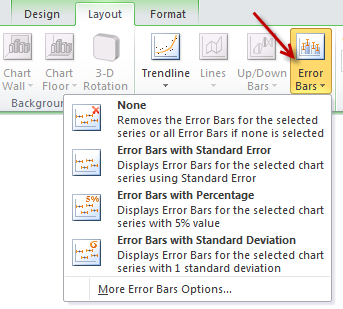
Repeat for Q3 series as well.
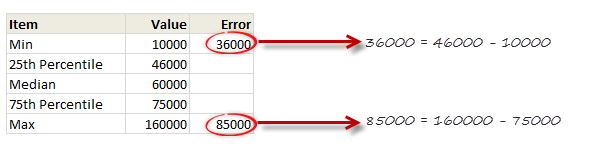
Step 7: Set up error values in your data
Add an extra column in your data area and use simple formulas to calculate error values, like below:
Step 8: Set up custom error values for Q1 & Q3
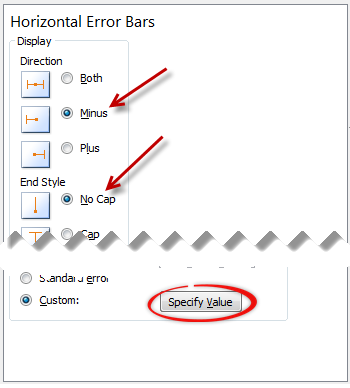
Select the error bar for Q1 (25th percentile) and,
- Press CTRL+1 to format them
- Enable only minus (negative) error bar with no cap.
- Select Custom as error amount and point to the calculated value.
Repeat for Q3, but choose positive error bar instead.
Step 9: Format the box plot to your taste
Remove any legend, axis, labels that you do not need. Change colors to suit your taste and mood. Make the whiskers subtle and knock off the grid lines. You are good to go.
Making Box plots interactive
Since box plots are very useful to understand distribution of values, we use them in dashboards etc. Naturally, you are interested to know how values are distributed for various things.
In this example, we may want to know how analyst salaries compare with manager salaries.
To make things complicated, we have 10 different job types, thus enabling 45 possible comparisons (10c2)
This is where interactive box plots can help. See this demo to understand:
Interactive Box plot in Excel – a Demo
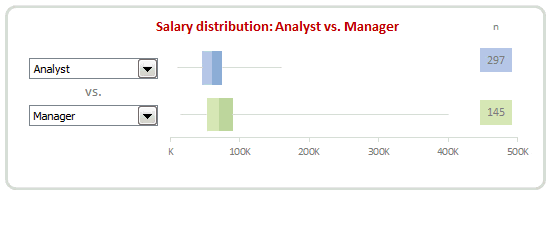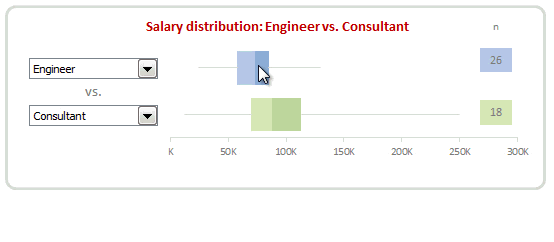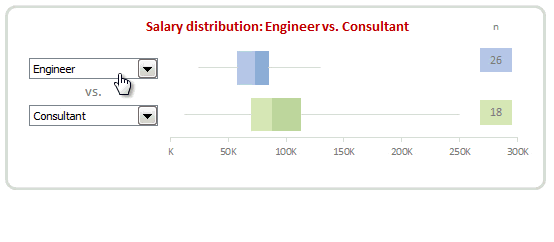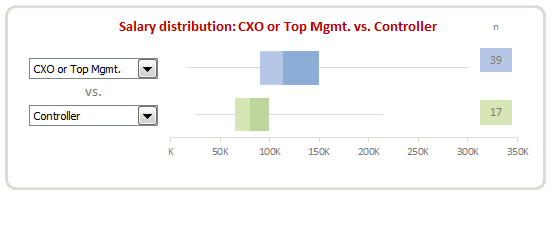
How to make interactive box plot in Excel
Construction of box plot is same as mentioned above. The difference is in adding interactivity.
Step 1: Use combo box form controls to capture comparison criteria
Excuse the tongue twister. Using Developer ribbon > Insert > Form controls, add 2 combo box controls and point them to the list of job types.
Lets assume that these combo boxes are linked to cells D1, D2.
[Related: Introduction to Excel Form Controls]
Step 2: Calculate 5 number summaries using MINIF, MAXIF and PERCENTILEIF formulas
Don’t rush to type the formulas yet. There is no such formula as MINIF (or MAXIF or PERCENTILEIF). Assuming your list of jobs are in joblist, write
=MIN(IF(joblist=”Analyst”, list_of_values,””))
and press CTRL+Shift+Enter
Using MAX(IF(…)) and PERCENTILE(IF(…)) you can calculate remaining 4 summaries.
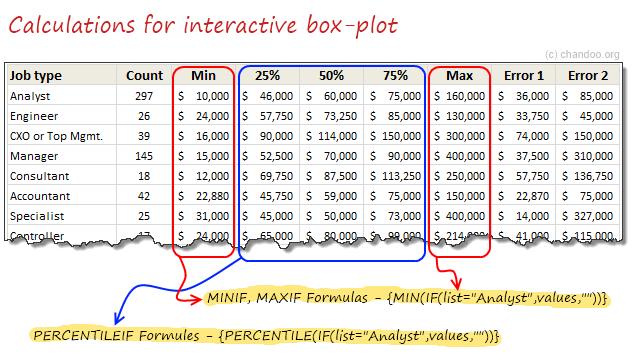
Step 3: Based on combo box selection, fetch any two sets of values
Using INDEX formula, we can fetch values corresponding to each combo box selection to a set of cells, like this:
Step 4: Connect these values to your box plots
That simple!
Step 5: Format and interact
Format the charts. Play with combo boxes to interactively compare one set of distribution with another. Show it to your boss or client and see them fall off a chair.
Download Box plot tutorial workbook
Click here to download the workbook containing these examples. Play with it. Check out various formulas and chart settings. Learn.
Do you use Box plots?
I love box plots. I have used them several times. Few examples are here: Excel age survey results, Gantt box chart and more.
In our Excel salary survey contest too, many people have used box plots to clearly compare compensation composition. Checkout the entries by Aditya, Allred, Anchalee, Anup, Bryan, Jeanmarc, Joerg, Kostas, Luke, Michael, Nathan, Sergey and Vishwanath. Especially Jeanmarc used interactive version of box plots to allow comparison on demand.
What about you? Do you use Box plots often? How do you prepare them? What is your experience like? Please share using comments.
Create Box plots often? Use Jon’s Add-in
If you need to create box plots often and find the above process tedious, then please consider getting a copy of Jon Peltier’s Box Plot add-in for Excel. It works like a charm and produces what you need. All in a few clicks. Click here to know more.
PS: Link to Jon’s add-in is an affiliate link. It means, when you buy it from Jon thru this link, I will get a few bucks too. I recommend it because I know it is awesome and perfect for box plots.
39 Responses to “11 very useful excel keyboard shortcuts you may not know”
You asked about a favorite keyboard shortcut: I often right click the navigation arrows at the bottom of an Excel workbook to get a list of the worksheets. I can click the one I want without having to scroll left or right.
I regularly use the networkdays(x,y,z) function to show the number of working days between two given dates. To exclude public holidays I reference a list of dates ("z" in the above reference) which I periodically update to reflect upcoming non-working days. To keep the sheet looking tidy for other users, I like to hide this column when I'm done, and then unhide it when I update the sheet.
With 40 separate workbooks to edit, these shortcuts make it a breeze...
? Hide selected column: CTRL+0 [zero]
? Unhide hidden column(s) within selection: CTRL+SHIFT+) [closed parenthesis]
If an "Autofit Selection" keyboard shortcut (not just a key sequence) existed, I'd be as happy as a clam!
you can use Alt+o+c+a to autofit selection
Is there a way to auto arrange the column width as you enter the data. Without a macro
You may use alternative key of hide the selected cell by ---print + H key
Unhide---prnt+U keys
You may use alternative key of hide the selected cell by ---print + H key
Unhide---prnt+U keys
[...] 11 very useful excel keyboard shortcuts you may not know [...]
[...] 11 very useful excel keyboard shortcuts [...]
[...] an Excel Conditional Formatting Rock Star 11 very useful excel keyboard shortcuts 73 Free Designer Quality Excel Chart Templates Tracking mutual fund / Stock portfolios using Excel [...]
Hello Chandoo, thanks for sharing this information. With some of the shortcuts I seem to have difficulties as they do not seem to work on the German keyboard.
Can you maybe verify that those combos are only working with the keyboard setup you are using? What would be a good source to lookup combinations for other layouts?
Regards, 1xoid1
@1xoid1 ... Thanks for visiting PHD and taking timeout to ask your question. Unfortunately all my German can be summarized to one phrase: "guten tag".
I wont be able to help you, but I can request other readers to respond. So if you know German or use German keyboard and can answer 1xoid1's question, then you get a free donut.
Guten Tag 🙂
To Sam Krysiak.
Shortcut to Autofit Selection (assuming you mean autofit columns). If you right click toolbar, click customise. From Commands tab/Categories select Built-in Menus.
In Categories window scroll down and select Columns and drag drop it onto toolbar. Then click the new toolbar Columns button and drag drop Autofit button onto your toolbar (note Autofit for Columns will no longer appear in your menus, only on toolbar).
Remove Columns button from toolbar (if you want to keep clutter down) drag and drop it off of your toolbar.
Close Customise box.
Now to Autofit columns just press "Alt" then "A".
Comment 8 correction - 2nd paragraph should read
"In Commands window...
@1xoid1:
Read the following text as follows: The key ,[;] is the one right to the M on the German keyboard. Here are the differences you have to know when using a German keyboard:
2. Press strg .[:] for inserting the current date (and strg shift .[:] for inserting current time)
3. Press strg ,[;] to copy values from cell above
8. Press strg shift –[_] to apply an outline border
10. Press strg-shift S to activate the font drop down (Schriftgroesse)
11. Press strg-shift G to activate the font size (Groesse)
Number 10 and 11 do not work with Excel 2007 anymore, but strg-shift-P shows the font tab of the cell format dialogue in Excel 2007.
All other shortcuts should work on a German keyboard exactly as Chandoo described them.
More information needed? Download a complete list with all shortcuts for Microsoft Excel in German (for free):
http://www.freeware-download.com/downloaddetails/5655.html
@Chandoo: please do not send a donut, unless you are able to attach one to an email. Otherwise the donut might be able to walk by itself, when it arrives here in Germany...
I forgot to mention:
For all readers using an English keyboard: Chip Pearson offers a comprehensive list of Excel shortcuts on the English keyboard:
http://www.cpearson.com/excel/ShortCuts.aspx
[...] your own keyboard shortcuts in Excel 2007, knowing a few keyboard shortcuts in excel is a huge help. Lyte Byte describes a nifty way to create your own key board shortcuts in [...]
[...] Select a bunch of cells and click on the Sigma symbol on the standard tool bar. Alternatively you can use Alt+= keyboard shortcut. [...]
I do some data entries column A,column B ,Column C , A and B have 10 to 12 digit codes , C has the names ; Kindly suggest me a format or formula for excel to avoid duplication of entries in all the the three columns.
Regards,
Prashant
@Prashant... You can use conditional formatting to highlight duplicate entries in the three columns. That way whenever you type a dupe value in a cell the formatting would highlight the values so that you can avoid the error.
check this post for more on using this way to handling duplicates: http://chandoo.org/wp/2008/03/13/want-to-be-an-excel-conditional-formatting-rock-star-read-this/
If you are looking for a way to remove duplicates from an existing range, you can try one of the various techniques we have described here. Try these tips:
http://chandoo.org/wp/2008/11/06/unique-duplicate-missing-items-excel-help/
http://chandoo.org/wp/2008/08/01/15-fun-things-with-excel/
[...] good alternative (although manual) is to use keyboard shortcuts CTRL + ; or CTRL + : to insert current date and time in the active cell. Since this places the [...]
Your site doesn't correctly work in safari browser
Hi GesyimmeliA: Can you tell me which version of Safari on which OS has this problem. I use Macbook at home and loaded the site quite often in Safari and never seen any layout or content issues. Are you facing any script issues while posting comments or somethings like that ?
Hey Chandoo. Great site. Learning lots.
My favorite Excel shortcut has got to be Alt+Down when over an autofilter drop down. Learning that changed my life. That was one of the last things I needed to use a mouse for. Changed my life.
[...] are a big advocate of keyboard shortcuts. I think learning a handful of keyboard shortcuts can improve your productivity tremendously, [...]
My favourit keyboard shortcut is control and 1 (use the 1 above the letters on the keyboard, not the number pad) for format cells.
Favourite shortcut: alt + shift + right/left arrow for grouping/ungrouping!
[...] Select a bunch of cells and click on the Sigma symbol on the standard tool bar. Alternatively you can use Alt+= keyboard shortcut. [...]
[...] clicking on these: excel keyboard shortcuts, excel mouse tips & tricks, excel productivity tips part 1 & part [...]
Martin Williamson thanks for the autofit tip! You rock.
In order to generate charts/bar graph with a single key:
1. Select the data
2. Press F11
3. Magic.... 🙂
F3 = Paste a Name or the entire list of Names
Crtl + F3 = Name Manager
Crtl + : = Inserts current time.
F12 = Save As
Mistake!
Crtl + Shift + : = Inserts current time.
SIR U R THE BEST PERSON WHO SHARES A WONDERFULL AND IMPORTANT TIPS IN EXCEL. THANKS AND KEEP ROCKING.
How do i hide / unhide a work sheet using the keyboard.
Great!
Other useful excel shortcuts
http://webtutorialplus.blogspot.com/2012/01/excel-quick-tip-useful-encoding-hotkeys.html
input in one cell 1a23bc output in two cell one of 123 and other one is abc how to possible, please help me.
Hey cool shortcuts but excel have more shortcuts then you listet.
i find a big database of supportet shortcuts for Excel 2007 here
http://www.veodin.com/excel-2007-shortcuts/
[...] INTEREST Date with my sheet – 10 tips on using date / time in excel http://chandoo.org/wp/2008/07/29/excel-keyboard-shortcuts/ [...]
Great article with some very useful follow-up comments and tips.
One simple question … how do you vertically align the drop-down filter button in a cell with a larger than normal height?
It’s easy enough to do so with a cell’s contents but the drop-down filter button stubbornly remains at the bottom and I need it at the top!
I’ve looked everywhere and haven’t located an explanation to what I am sure is considered an Excel basic.
Cheers