Last week, we had an interesting homework problem – What is the average speed of this road trip?
We received more than 150 answers. But to my surprise, 57 of them are wrong. So today, lets learn how to calculate the average speed correct way.
Please click here to download solution workbook.
What is Speed?
Back in school days, we learned what speed is.
Speed = Distance / Time
Now lets look at the problem
Here is the data:
Jack kept track for every 50 mile interval. And he did that for 12 intervals. So the total distance is 12×50 = 600 miles.
We just need to know how much time Jack took to cover the 600 miles to calculate the speed.
We know that Jack covered first 50 miles @ 43mph.
So the time taken for first 50 miles is 50/43 = 1.16 hrs (or 1 hr & 9 mins)
Like wise, if we calculate times taken for all the 50 miles, we get this:
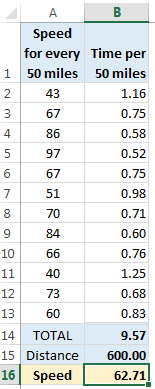
Isn’t there a way to calculate this without helper column?
Now you are talking.
While the detailed break-up of the calculation above helps us understand how Time, Speed & Distance are related, when answering a question like “What is Jack’s average speed?”, you may want to write a single formula to get the answer (instead of all the extra helper column cells).
The range A2:A13 contains speeds per 50 mile intervals.
The time taken for first 50 mile is =50/A2
The time taken for second 50 mile is = 50/A3
…
So, 50 / (A2:A13) should give us an array of times.
And the total time taken is a simple sum of this array.
So, SUM(50/(A2:A13)) should give the total time.
Now, if we divide 600 by this, we should get our average speed for the entire trip.
Formula #1: Array SUM()
Our first formula for calculating average speed is,
=600 / SUM(50/(A2:A13))
Since this is an array formula, you should press CTRL+Shift+Enter to get it work.
Formula #2: SUMPRODUCT
While the above formula works beautifully, it is a bummer that we must press CTRL+Shift+Enter to get it work. Why not use a formula that can natively process arrays.
Enter SUMPRODUCT.
=600 / SUMPRODUCT(50/(A2:A13))
works just as beautifully and you don’t have to press CSE.
Formula #3: Harmonic Mean
Lets expand the formula and see what is happening, mathematically speaking.
Our formula is,
=600 / SUM ( 50 / (A2:A13) )
in mathematical terms, this is,
= 600 / ? [ 50 / (A2:A13) ]
= 600 / [50/A2 + 50/A3 + 50/A4 + … + 50/A13]
After isolating 50, we get:
= 600 / [50 * (1/A2 + 1/A3 + 1/A4 + … + 1/A13)]
= 12 / (1/A2 + 1/A3 + 1/A4 + … + 1/A13)
Lets call this blue expression as (1).
Time for introducing the concept of Harmonic Mean.
The harmonic mean is the reciprocal of the arithmetic mean of reciprocals.
Sounds confusing?!?
Take a sip of that coffee and read again.
reciprocal of the arithmetic mean of reciprocals
So harmonic mean of a range of numbers (say a,b,c,d…) is
=1/ [(1/a + 1/b + 1/c +…) / (count of numbers)]
or in other words,
= count of numbers / sum of reciprocals
Applying this concept to the range A2:A13, we get
= count of range / sum of reciprocals of A2:A13
= 12 / (1/A2 + 1/A3 + 1/A4 + … + 1/A13)
Now, isn’t the red expression of harmonic mean same as the blue expression (1) above?
Thus, to calculate the average speed, we just need harmonic mean of the the range A2:A13.
And there is a perfect formula for that.
=HARMEAN(A2:A13)
So, we can use that and it gives average speed for the trip in one step!
Special case – What if the speed is not tracked at equal distances?
 Lets say Jack measured his speed at 40,50,60,40,60,50,40,50,60,60,50,40 mile intervals instead of every 50 miles.
Lets say Jack measured his speed at 40,50,60,40,60,50,40,50,60,60,50,40 mile intervals instead of every 50 miles.
In such case, we can’t use HARMEAN() because the distances are not equal. Fortunately, we can still use SUMPRODUCT.
Assuming the distance covered per interval is in the range B2:B13 (speeds are already in A2:A13),
The formula,
=SUM(B2:B13)/SUMPRODUCT(B2:B13/A2:A13)
tells us the average speed of the trip.
Learn more: Calculating weighted average using SUMPRODUCT.
Download the solution workbook
Click here to download the solution workbook. Examine the formulas to learn more.
As a bonus, It contains an additional problem to test your skills.
A twist in the tale – Tracking time instead of speed
Lets say after all this formula struggle, Jack (our driver of the road trip) wised up and started tracking time instead of speed. So his new log looks like this:

Now how do we calculate the average speed?
The time stamp data is in range A2:A16 and distance is in B2:B16.
Please post your formulas in the comments section.
PS: The solution workbook contains answer to this problem as well. Just unhide to see.
Go ahead and post your answers. This time, lets hope we get fewer than 1/3rd answers as wrong.
Learn more about formulas:
Check out any article from our formula forensics or Excel homework pages to learn something interesting & cool. Also go thru SUMPRODCUT & Advanced SUMPRODUCT articles to sharpen your formula writing skills.
Listen to our podcasts on averages to raise above your average.





















12 Responses to “What is the average speed of this road trip? [Solution & Discussion]”
Average excluding breaks = 48.85mph
=MAX(B2:B20)/((+MAX(A2:A2) - MIN(A2:A20))*24)
(I've done it as a range so that it cope with more/fewer records)
Struggling with the average including breaks as a single calculation. Using a number of helper columns I get an aswer of 56.51mph
Oops - typo in the formula! Try
=MAX(B2:B20)/((MAX(A2:A20)-MIN(A2:A20))*24)
I did it the long way. And not very automated. But I got the answers.
=MAX(B2:B16)/((A16-A2)*24)= 48.85
=MAX(B2:B16)/(((A16-A2)-(A6-A5)-(A9-A8)-(A12-A11)-(A15-A14))*24) = 56.51
Hi,
I'm not the brightest so how do you convert the 1.16 to show actual duration of time such as 1:09?
@Tail: 50/43 give a decimal duration of 1.1628 hours. If you format this answer as hh:mm will give you a figure of 3:54:25. This is because in date formats, numbers are seen as the number of days, so .16 (just under one sixth) of a day is just under 4 hours.
Therefore to see 1.16 as a time duration in hours, divide by 24 - 50/43/24 = 1:09
Average time including breaks
=B16/((A16-A2)*24) = 48.84668
Average time excluding breaks
=B16/SUMPRODUCT((((B3:B16-B2:B15)>0)*1)*(A3:A16-A2:A15)*24)
= 56.51491
very interesting but too much confusing.
@Rita
I'll try a formula forensic for you!
=B16/SUMPRODUCT((((B3:B16-B2:B15)>0)*1)*(A3:A16-A2:A15)*24)
(B3:B16-B2:B15) - from cell b3 onward this takes the distance covered and subtracts from it the previous reading (giving a distance covered since the last measurement) and gives us an array {43;46;34;0;76;0;137;37;0;80;25;0;76}. Note that the zeros show where their was a rest period.
((B3:B16-B2:B15)>0) – this takes the array above and checks if each value is greater that 0. This gives us an array {TRUE; TRUE; TRUE;FALSE; TRUE; TRUE;FALSE; TRUE; TRUE;FALSE; TRUE; TRUE;FALSE; TRUE;}
((B3:B16-B2:B15)>0)* 1 – this is a clever trick to turn TRUE/FALSE into numbers – 1 for TRUE and 0 for FALSE. This gives us an array {1;1;1;0;1;1;0;1;1;0;1;1;0;1;}
(A3:A16-A2:A15) – from cell a3 onwards this takes the time value and subtracts from it the previous time value (giving the elapsed time as a decimal of a day) – giving and array {0.04166;0.03472;0,02777;0.01666;0.03194;0.07430;0.02013;0.08611;0.02708;0.00694;0.05486; 0.02083;0.02569;0.04305} (I’ve truncated it to 5 decimal places to make it easier to read)
Now we multiply our two arrays together – this will give us the time intervals excluding the rest periods (anything multiplied by zero equals zero). Our resulting array is all of the time intervals excluding the rest periods) –{0.04166;0.03472;0,02777;0;0.03194;0.07430;0;0.08611;0.02708;0;0.05486;0.02083;0;0.04305}
We really want the time interval to be in hours. Therefore we multiply the array by 24 giving a result of {0.9999;0.8333;0.66666;0;0.76666;1.78333;0;2.06666;0.65000;0;1.31666;0.49999;0;1.03333}
SUMPRODUCT is a great way of totalling entries in an array – this gives a total time interval of 10.6166 hours (excluding the break stops)
The average speed is therefore 600/10.61666 giving a result of 56.51491 mph
Kudos for the beautiful explanation Robert.
Help me understand this, please.
Column A clearly spells out "SPEED FOR EVERY 50 MILES". Why don't we just do average A2:A13?
@New and Confused
Speed = Distance / Time
or rearranged
Time=Distance/Speed
Using the first segment as an example
Speed = 43 MPH
and we know the Distance is 50Miles
thence the Time for that segment is: 50/43
=1.16 Hrs
Now we repeat that for the 12 sections
We know the total distance is 12 * 50 = 600 Miles
and the sum of the times calculated above is 9.57 Hrs
Hence the Average speed is = Distance / Time
=600/(9.57)
=62.71 MPH
The average of the averages is 67 MPH which is incorrect
If You average 67 MPH for 600 Miles the time taken would be
Time=Distance/Speed
= 600/67
=8.96 Hrs which is also wrong
This is awesome. For all the TSD (Time Speed Distance) rallyists out there, this spreadsheet is a godsend!!! Just enter your speeds from the speed charts and follow the time. No need to get your calculator.
Just make sure your driver is telling you the correct odometer reading.