Today, lets learn how to make a simple timer app using Excel. First some background…,
Recently, I learned how to solve Rubik’s cube from my nephew. As a budding cuber, I wanted to track my progress. Initially I used the stopwatch in my iPhone. But it wont let me track previous times. So I thought, “Well, I can use Excel for this”.
So I made a small timer app using Excel. Its quite minimalistic. It has a single button. I press it and it tracks the start time (date & time stamp). If I press the button again, it records the duration.
This way, I can see my progress over next few weeks and may be plot the trend.
Demo of the Excel VBA timer
Here is a short demo. This is what we will be building.
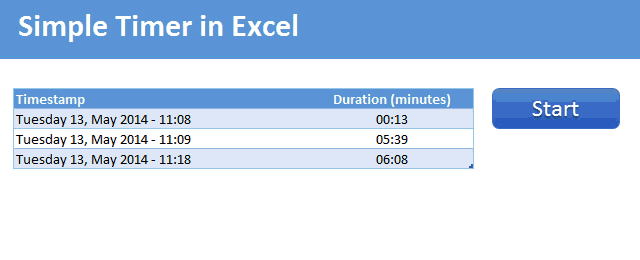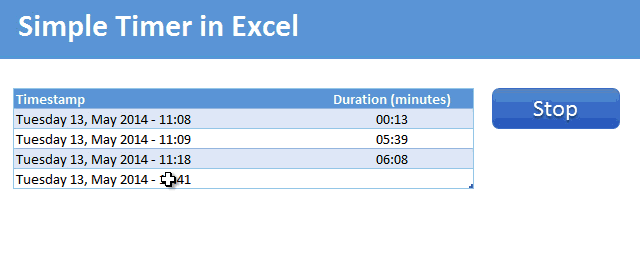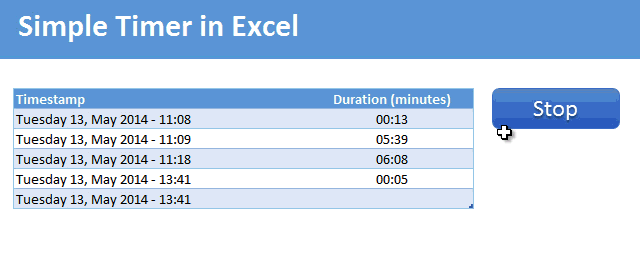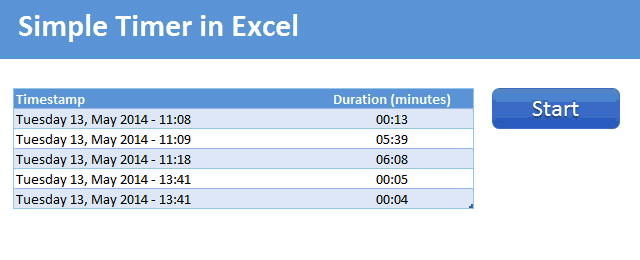
Tutorial to make a timer in Excel
To make a timer app in Excel, first we need to understand the logic for this. If VBA apps can be defined on a scale of 1 to 10 (1 being easiest to develop and 10 being most complex), our timer app can be classified as 1.5. It is really simple. But nevertheless, it is a good idea to list down various ingredients and basic logic to follow.
So we need,
- A table to store the time stamps & durations
- A button (simple text box will do) to start & stop the timer
Set up the timer worksheet
In a blank worksheet, make space for a 2 column table. Type Time stamp & Duration as column headings and make a table from these (CTRL+T to insert the table)
Note: For the macro to work, you do not need a table. Any 2 column range will do. A table makes our timer app look sexy.
Also, insert a rounded rectangle and format it to look like a button (from Format Ribbon > Shape Styles, select something slick and pretty)
In a blank cell, type the word “Start”. Name this cell as timer.button.label
Now, click on the rounded rectangle button, go to formula bar and type =timer.button.label
💡 Tip: Yes, you can assign names or cell references to shapes. This way, whatever text is in the cell will be shown inside the shape.
Other names to make:
Although we can write VBA code without creating these names, our code will be readable with these names. So here we go:
- Select the header “Timestamp” of the table and name it as time.stamp.start
- Name the table as Durations from Table Design ribbon
- In a blank cell, write the formula =COUNTA(Durations[Timestamp])
- This counts how many timestamps are already inserted.
- Now name this cell as count.of.timestamps
We are done. Lets roll in to VBA.
Writing the VBA code for timer
Open VBE (Visual Basic Editor) and insert a new module in your timer workbook. There write this code.
Sub startStopTimer()
If Range("timer.button.label") = "Start" Then
Range("time.stamp.start").Offset(Range("count.of.timestamps") + 1).Value = Now
Range("timer.button.label") = "Stop"
Else
Range("time.stamp.start").Offset(Range("count.of.timestamps"), 1).Value = Now - Range("time.stamp.start").Offset(Range("count.of.timestamps"))
Range("timer.button.label") = "Start"
End If
End Sub
Assign this macro to the timer button
Right click on timer button and choose “Assign macro”. Select the startStopTimer sub from the list and click ok.
Now go ahead and test it. Assuming you have used same names as per this post, your timer should work.
How this macro works?
When you click on the timer button, you want one of the 2 things to happen.
- You want to start the timer
- You want to stop the timer
What you want to do can be checked with this logical check.
Range("timer.button.label") = "Start"
If this is true, then you want to start the timer.
Else, you want to stop the timer.
If you want to start the timer
Then, we need to go to the last row of the table + 1 and insert current time (now) in that cell.
This is done by,
Range("time.stamp.start").Offset(Range("count.of.timestamps") + 1).Value = Now
Once we do that, we need to change timer button’s text to “Stop”.
This is done by,
Range("timer.button.label") = "Stop"
If you want to stop the timer
Then, we need to go to the last row’s 2nd column of the table and print the difference between latest time (now) and starting time (last row, first column value)
This is done by,
Range("time.stamp.start").Offset(Range("count.of.timestamps"), 1).Value = Now - Range("time.stamp.start").Offset(Range("count.of.timestamps"))
Once we do that, we need to change the button text to “Start” by using this code:
Range("timer.button.label") = "Start"
That’s all. Our VBA code is rather simple.
One last step, formatting the duration
If you look at the duration, it could read something like 0.0042354. This is because duration is displayed as a fraction of day. So 0.0042354 means the duration is 0.42% of a day.
Now, wouldn’t it be better if we can show this in minutes and seconds?
To do that, select the entire table column of durations, press CTRL+1
Then, set formatting as custom and type code as [mm]:ss
And you are done!
Download Simple Timer Excel VBA workbook
Click here to download Simple Timer Excel VBA workbook. Play with it. Use it to track your Sudoku, crossword or knitting times. Or even Rubik’s cube times. See what trends and patterns you can uncover.
Do you use Excel for tracking time?
I know many companies use Excel based trackers to keep track of employee time. I personally use time tracking features of Excel for needs like this all the time.
What about you? Do you use Excel time functions like NOW, TODAY and VBA to track progress? What techniques you apply? Please share using comments.
Like tracking? You will love these
If you track things with Excel, you are going to find below tutorials very useful.
- Tracking issues & risks – Project management
- Tracking to dos – Project Management
- Expense tracker using Excel – 7 templates
- Annual goals tracker
- Bonus: Introduction to VBA – 5 part crash course
Note: Rubik’s cube image by Booyabazooka thru Wikimedia
129 Responses to “Write a formula to check few cells have same value [homework]”
=NOT(STDEV(A1:A4))
this also works for large ranges of numerical values (but not for text)
@Arie
Nice formula Arie
Except that it doesn't work for Text values
I'll submit
=COUNTIF(A1:A4,A1)=COUNTA(A1:A4)
which works for Numbers and Text
and answers the two bonus questions as well
This is waaay more elegant than my solution. Nice one :).
I had =NOT(COUNTIF(A1:A4,A1:A4)-COUNTA(A1:A4)), somehow I keep forgetting we can use more than one "=" sign on a given formula :-/
Hi
Works for numbers, text and logical values on a range from A1:An.
=COUNTIF(A1:An,A1)=ROWS(A1:An)
well if you name the range, you could use following:
=IF(SUMPRODUCT(1/COUNTIF('range','range'))=1,1,0)
Hello lockdalf
The IF()-part is not necessary.
=SUMPRODUCT(1/COUNTIF(‘range’,'range’))=1
Not Working for =IF(SUM($C$1:$F$1)=0,"",SUM($C$1:$F$1)) in cell A1 to A4
My solution is a, perhaphs slightly complex, array formula as follows:
{=IFERROR(AVERAGE(IF(ISBLANK(A1:H1),9999,SUBSTITUTE(A1:H1,A1,9999)*1))=9999,FALSE)}
Assuming there is a value (numerical, text, logic etc) in cell A1, this formula will work - and it will 'ignore' any cells that are 'blank' within the range A1:H1 (which can be extended to the required size).
Breaking the formula down, the SUBSTITUTE(A1:H1,A1,9999) replaces all values (be it text / numerical) in the range A1:H1 that MATCH the value of cell A1 with the number 9999 (this should be changed to any number that WON'T APPEAR IN THE RANGE).
These values are then multiplied by 1 (as SUBSTITUTE results in a text answer).
Wrapping this in an IF(ISBLANK(A1:H1),9999,.........) formula takes care of any blank cells, setting them to this default value of 9999 also - this allows you to set the formula up once for a large range and then not have to alter as more data comes in.
An Average is then taken of all these values - if all cells that contain values are the same, the average will come back to 9999.
If all values are numerical but some differ, the average will differ from 9999 and will result in a FALSE answer. If some / all of the values are text and some differ from that in cell A1, the AVERAGE function will result in an Error, but in these instances the Match needs to return FALSE, hence the IFERROR function.
Sure there's a simpler way to do this though!!
`{=IF(AND(COUNTA(RANGE)-SUM(--ISNUMBER(FIND(UPPER(FIRST ELEMENT IN RANGE),UPPER(RANGE))))=0,LEN(FIRST ELEMENT IN RANGE)=MAX(LEN(RANGE))),TRUE,FALSE)}`
so if your data was in Column 1 and began in A1, you'd use
`{=IF(AND(COUNTA($1:$1)-SUM(--ISNUMBER(FIND(UPPER($A$1),UPPER($1:$1))))=0,LEN($A$1)=MAX(LEN($1:$1))),TRUE,FALSE)}`
This will work for strings and things, if you want it to be case sensitive (I don't), just remove the UPPER() part.
What this does:
`COUNTA($1:$1)`
tells you how many entries you're looking at over your range (so we can work with an undetermined size).
`--ISNUMBER()`
ISNUMBER will return TRUE or FALSE depending on if the value inside is a number or not. the -- part converts TRUE/FALSE in to 1 or 0.
`UPPER()` OPTIONAL
converts the value in to upper case. If passed a number it changes it to text format. This is what stops it from being case sensitive.
`FIND($A$1,$1:$1)`
will return a number if A1 is contained in each cell containing an entry in column 1.
`LEN($A$1)=MAX(LEN($1:$1)`
checks that all elements are the same length. This is needed to avoid partial matches (without it, if A1 contained zzz and A2 contained azzza it would flag as true).
REMEMBER this is an array formula, so enter with ctrl+shift+enter.
{=MIN(--(A1=OFFSET(A1,,,COUNTA(A1:A4))))}
Gives 0 if false and 1 if true
=COUNTIF(A:A,A1)/COUNTA(A:A) = 1
This meets both bonus requirements and is dynamic. Keep adding more contents in column A and it will include these automatically.
I like this a one a lot. I would make one small change by inserting a table for my data range. Makes it dynamic without selecting the whole column
=IF(COUNTIF(tableName[colName],A2)/COUNTA(tableName[colName])=1,TRUE,FALSE)
For only Numeric values
=MAX(A:A)=MIN(A:A)
Awesome!
=(A1=B1)*(B1=C1)*(C1=D1)
Case sensitive.
=SUMPRODUCT(0+EXACT(A1:A4,A1))=COUNTA(A1:A4)
Regards
I'd use this
=COUNTIF(range,INDEX(range,MODE(MATCH(range,range,0))))=COUNTA(range)
It takes Hui's formula but ensures that the test value for the countif is the value or string that is most common in the range. Just in case you get a false but the problem is just with your test value being the odd one out.
=SE(E(A1=A2;A1=A3);SE(E(A1=A4;A2=A3);SE(E(A2=A4;A3=A4);"ok")))
SE = IF
E = AND
Seems you could shorten it with
=AND(A1=A2,A1=A3,A1=A4)
Bonus question 1 & 2
Array formula: {AND(A1=A1:AN)}
This will test all cells in range, including text and numbers.
Cheers
A very simple solution uses Excel's Rank function. Insert in B1 = Rank(A1, $A$1:$A$4). Copy down this formula to B4. If the answers in B1 thru B4 are all 1, the values are equal. For an open range of cells, label the range of input (example "TestData") and place the label in the funtion (= Rank(A1, TestData) then copy down to an equivelent length of rows as the range.
=IF(SUM(A1:A4)/COUNT(A1:A4)=A1,TRUE,FALSE)
=IF(SUM(A1:D1)/4=A1,"True","False")
I enjoy your emails. I have learned a lot from them. Thank you for what you do.
.
{=PRODUCT(--(A1=A1:A4))}
.
Change A4 to An.
Greate
{=PRODUCT(- -(A1=A1:A4))}
=IF((SUM(A1:A4)/COUNT(A1:A4))=A1,"TRUE","FALSE")
I would use the formula which is mentioned below:-
=IF(PRODUCT($A:$A)=A1^(COUNTIF($A:$A,A1)),"Yes","No")
At last a homework assignment that I could answer on my own. And I even understand some of the elegant answers from other readers this time.
My solution was to nest IF statements:
=IF(A4=A3,IF(A3=A2,IF(A2=A1,TRUE,FALSE),FALSE),FALSE)
This satisfies bonus question 2 but I think the structure makes it impossible to modify this solution to satisfy bonus question 1. And I wouldn't want to use this strategy to compare very many values...
This answers all of your questions:
=PRODUCT(--(INDIRECT("$A$1:$A$"&$B$1)=$A$1))
where column A contains the values and $B$1 has the number of rows to assign to last A-cell.
Sorry, forgot the braces:
{=PRODUCT(–(INDIRECT(“$A$1:$A$”&$B$1)=$A$1))}
=IF(A1=A2:A2=A3:A3=A4>1,"TRUE","FALSE")
=IF(A1=A2:A2=A3:A3=An>1,"TRUE","FALSE")
=SUM(HELLO, A1)
{=IF(SUM(IF(A1:A4=A1,0,1))=0,TRUE,FALSE)}
This will work for numbers or text, and will work for any number of cells (A4 would just be An)
Here's another alternate, assuming values in cells a1:d1
=IF((A1*B1*C1*D1)^(1/COUNT(A1:D1))=AVERAGE(A1:D1),1,0)
{=IF(AND($A$1:$A$4=OFFSET(A1,0,0)),1,0)}
=SUM(IF(FREQUENCY(MATCH(A1:A4,A1:A4,0),MATCH(A1:A4,A1:A4,0))>0,1))
REVISED FORMULA
=IF((A1=A2)*AND(A1=A3)*AND(A1=A4),"TRUE","FALSE")
Regards
=IF(SUMPRODUCT(--(A2:A5=A2))/COUNTA(A2:A5)=1,1,0)
- should be --
I would use something like this: =COUNTA(A1:A4)=COUNTIF(A1:A4,A1)
You can even do a whole range and as you enter data into the range it tells you if they all match. Going down to row 5000: =COUNTA(A1:A5000)=COUNTIF(A1:A5000,A1).
Thanks,
B
Just saw Hui response. I really did come up with this and didn't just copy his.
{=SUM(--(A1:A101=A1))=(COUNTA(A1:A10)+COUNTBLANK(A1:A10))}
For numeric values:
=(OFFSET(list,,,1,1)=AVERAGE(list))
where list = A1:A4
I need to retract my own post here guys.
It is WRONG! Let me explain.
Suppose we have
A1 = 1
A2 = 0
A3 = 2
then Average = 1 and OFFSET(list,,,1,1) = 1
so 1 = 1 but all the elements are NOT equal.
correction
{=SUM(--(A1:A10=A1))=(COUNTA(A1:A10)+COUNTBLANK(A1:A10))}
=IF(A1=B1,IF(B1=C1,IF(C1=D1,TRUE,FALSE),FALSE),FALSE) ....
=COUNTIF(OFFSET($A$1,0,0,COUNTA($A:$A),1),$A$1)=ROWS(OFFSET($A$1,0,0,COUNTA($A:$A),1))
I have a little more flexible approach. Suppose the value of 'n' is known. There is a possibility that only some of the cells in a row are filled up. For example if n = 10, then in a row, A1 to A10 must be compared. But in case only cells upto A7 are filled up. The formula thus has to adapt accordingly. Below formula does that:
=COUNTIF(INDIRECT(ADDRESS(ROW(),1)&":"&ADDRESS(ROW(),COUNTA(A1:J1))),A1)=COUNTA(INDIRECT(ADDRESS(ROW(),1)&":"&ADDRESS(ROW(),COUNTA(A1:J1))))
In A1:A100 is word/number
In B1 is word/number we look
C1=MAX(FREQUENCY(IF(A1:A100=B1,ROW(A1:A100)),IF(A1:A100<>B1,ROW(A1:A100)))) array formula
We can use an array formula
{=PRODUCT(--(A1:An=A1))}
OR if we want n variable
{=PRODUCT(--(INDIRECT("A1:A"&COUNTA(A:A))=A1))}
Just as an add on...
The range could be 2D as well
{=PRODUCT(–(A1:Zn=A1))}
{=AND(A1=A2:An)}
I would use this one (simlpe)
=(COUNTA(A:A)=COUNTIF(A:A;A1))
try this
=MAX(A1:A4)=MIN(A1:A4)
Olso try this
{=SUM(RANK(A1:A10,A1:A10))=COUNT(A1:A10)}
Please notice it is an Array Formula
Dear All,
i used that formula
{=IF(COUNTIF(A1:A4,A1:A4)=COUNTA(A1:A4),TRUE,FALSE)}
Love the variety of responses.
=MAX(A1:A4)=MIN(A1:A4)
and
=COUNTA(A1:A4)=COUNTIF(A1:A4,A1)
will return true if the input range has blank cells
My personal fave is the array formula {=AND(A1=A1:A4)}. Short and sweet, and easy to read. Blank cells will tally as a mismatch.
A close second is
=SUMPRODUCT(1/COUNTIF(A1:A4,A1:A4))=1
which will throw an error if blanks are present.
=PRODUCT(B1:D1)=B1^COUNT(B1:D1)...will return TRUE or FALSE
Dear Sir,
My answer is =exact(a2,a1)
=IF((a1=a2=a3=a4),1,0)
4 equal values gives me a 0 ???
Hello Chandoo,
We can also use Conditional Formatting......
For Numerics..
=SUM(A1:AN)/A1=COUNT(A1:AN)
results in True/False.
=AND(IF(A1=B1,1,0),IF(B1=C1,1,0),IF(C1=D1,1,0))
=AND(A1=A2:A4) array entered
Generic
=AND(A1=A2:An) array entered
=--(COUNTIF(A1:A4,A1)=COUNTA(A1:A4))
will give value as 1 or 0
Hi there, here's a simple formula to determine not only whether all 4 cells (A1 --> A4) are equal, but also whether any of the cells are equal and identifies which cells they are ...
=COUNTIF($A$1:$A$4,A$1)*1000+COUNTIF($A$1:$A$4,A$2)*100+COUNTIF($A$1:$A$4,A$3)*10+COUNTIF($A$1:$A$4,A$4)*1
A result of 1111 means no cells are equal, 4444 means all cells are equal, 1212 would mean there are 2 cells the same & they are in A2 & A4, etc
=((A1=B1)+(A1=C1)+(A1=D1))=3
Obviously doesn't cover bonus question 1, but does so for q2 🙂
If formula
=MIN(A1:A4)=MAX(A1:A4)
Try this formula
=IF(COUNTIF(A1:A4,A1)-ROWS(A1:A4)=0,"True","Flase")
I used the Swiss knife of excel: SUMPRODUCT, works for numeric as well as for non-numeric cell content and A1:A4 is obviously easily changed to any range.
=IF(SUMPRODUCT(--(OFFSET($A$1:$A$4,0,0,ROWS($A$1:$A$4)-1,1)=OFFSET($A$1:$A$4,1,0,ROWS($A$1:$A$4)-1,1)))=ROWS($A$1:$A$4)-1,TRUE(),FALSE())
All of the individual non-array formulas (didn't test the array ones) have one flaw or another - mostly specifically if all the columns are blank, the result would still be false.
Another formula in the comments worked for these but didn't work for when all columns had "0.00" in them. My solution was to OR the two. If H3 through H149 have your values, then this is what worked for me:
=IF(OR(COUNTIF(H3:H149,H3)=COUNTA(H3:H149),SUMIFS(H3:H149,H3:H149,1)=COUNT(H3:H149)),IF(H3="","Blank",H3),"")
This solution puts "Blank" if all the rows are blank, otherwise, it puts whatever the value that's in all of the rows - "0.00" or whatever.
Thanks for all the answers!
I used a nested if statement which also showed, via the false message, the first instance of cells which were not equal for the cells a1 to a5.
=IF(A1=A2, IF(A2=A3, IF(A3=A4, IF(A4 = A5, "True","False A4"), "False A3"), "False A2"))
Hi,
First, let me begin by saying, I am a big fan of all your posts and read your emails, mostly on the same day as you send them. I have not replied as much as I wanted to.
This is my first attempt at answering a question on your post
I came up with a simple check which will test if all values in a range A1:An are same or not
Assuming range you want to check is A1:A10,
In Cell B1, insert the formula
=IF(COUNTIFS(A1:A10,A1)=COUNTA(A1:A10),"All cells are same","All cells are not same")
The idea I applied is counting total number of non-blank cells and then counting the number of cells which match cell A1. If these are same, then it means
a) all cells have the same value! (All can be blank, then both counts will be zero)
I am working on finding the range automatically 🙂
Can extend this into VBA and use InputBox etc to generate some user interaction
Thanks
Shailesh
=IF(COUNTIF(A1:A4,A1)=COUNT(A1:A4),TRUE,FALSE)
For homework & Bonus Question 3
=IF(AND(A1=A2,A2=A3,A3=A4),1,0)
=IF(SUMIFS(A12:A15,A12:A15,1)=COUNT(A12:A15),1,0)
One possible solution could be =+IF(COUNTIF(A1:A4,A1)-COUNT(A1:A4)=0,1,0)
where A1:A4 is data range which can be a dynamic range and the formula can be modified accordingly.
Rgds,
Sanjeev Sawal
I got the right result with this one:
=IF(A1=B1;IF(C1=D1;IF(B1=C1;1;0);0);0)
=and(a1=a2,a1=a2,a1=a3)
ANSWER FOR bONUS 1
=MAX(A1:A10)-MIN(A1:A10)
=AND(A1:A3=A2:A4)..Confirm with Ctrl+Shift+Enter (As as array formula). Works well for Text values and large range of values as well.
suppose cells contain 2 values ==== Yes | no
formula :
1
=counta(a1:a4)=countif(a1:a4,"yes")
It will return True or False.
2
=IF((COUNTA(A1:A4)=COUNTIF(A1:A4,"yes")),"Same value","Mis-match")
it will return Same Value OR Mis-match.
Hope you like it.
Regards
Istiyak
Also can use this formula
=IF(AND(A1=A2,A1=A3,A1=A4),"1","0")
Let say the values are in the range $B$1:$E$1, then the formula is:
If(sumproduct(--($B$1:$E$1=$B$1))=CountA($B$1:$E$1);1;0)
Please check that:
* $B$1 was used as pivot value and could be randomly selected
* It works well if parenthesis is omitted for values "1" and "0"
* This formula applies also to "n-values" and non-numeric values (text, logical, etc.)
Regards,
A
This formula is equivalent to
If(CountIF($B$1:$E$1,$B$1)=CountA($B$1:$E$1),1,0) mentioned before...
Hi, first time trying to solve a probleme.
New at this but really enjoying Chardoo.org
Think the following will work in all 3 questions
{=IF(SUM(IF(A1=$A:$A,1,0))=COUNTA($A:$A),TRUE,FALSE)}
Regards
Jorrie
use below formula for to get True / False
=COUNTA(A1:A4)=COUNT(A1:A4)
and use below formula for to get {1/0} or {match / Mismatch}
=IF(COUNTA(A1:A4)=COUNT(A1:A4),{1,0} or {match,Mismatch})
=IF(COUNTA(A1:A4)=COUNT(A1:A4),1,0) or =IF(COUNTA(A1:A4)=COUNT(A1:A4),"Match","Mismatch")
[...] Last week in Write a formula to check few cells have same value [Homework], [...]
Hi, sorry if it's repeated, this array formula works well with numbers or text, the range can easily be dynamic: {=AND(A1:An=A1)} Now, after three days, I understand a lot more about array formulae, thanks?
=IF(AND(A1=A2,A2=A3,A3=A4),"TRUE","FALSE")
What if there are not only four cells to compare but An?
how will I determine if there is one cell that is not equal from any other cells?
=IF(COUNTA(A1:A4)=COUNT(A1:A4),1,0)
=IF(COUNTA(A1:A4)=COUNT(A1:A4),”Match”,”Mismatch”)+
=IF(AND(A1=A2,A2=A3,A3=A4),”TRUE”,”FALSE”)
=iF(AND(EXACT(C15,D15),EXACT(E15,F15)),"Match","Mis-match")
how this formula works in excel (B4+E4)/50*20
I'm a little late to the party, but I figured I'd post anyways.
For numbers only:
=NOT(VAR.P(A1:An))
The formula given below will fulfill the all criteria including bonus questions
=IF(COUNTA(A:A)=COUNTIF(A:A,A1),"True","False")
REGARDS
=IF(MATCH(A1,A2:A4,0),TRUE,FALSE)
=IF(COUNTIF($A$1:$A$4,A1)>1,"true","false")
=IF(COUNTIF(A:A,A1)>1,"true","false")
@Naveen
You can simplify your formulas as below:
=COUNTIF($A$1:$A$4,A1)>1
=COUNTIF(A:A,A1)>1
Excel will return True or False without the need for the If() function
Hi ,
This question is similar to the one in the post.
I have Text values in cell A1 and A2.
If A1 = A2, update 10 in cell A3 , else 0.
Is there any formula for this. I am new to VB and hence do not have much knowledge. Eager to learn!!
Thanks in advance !!!
=AND(A1=A2,A1=A3,A1=A4)
also =IF(AND(A1:A4=A1),TRUE,FALSE)
my question is
finding the total of values in cell A1,A2,A3,A4,andA5
@Norine
Is it as simple as =Sum(A1:A5)
One can use "IF, AND" formula.
=IF(AND(A1=A2,A2=A3,A3=A1),"True","False")
=COUNTIF(A:A,A1)=COUNTA(A:A)
Enter array formula like, = IF($B$16:$B$21=$B$17:$B$22,"Yes","No")
Sorry, Enter a array formula like this: =IF(AND($B$16:$B$21=$B$17:$B$22),"Yes","No")
=IF(AND($E$5=$E$6,$E$6=$E$7,$E$7=$E$8),"true","flase")
it can work try this one
A question for you
sheet 1 table A1:C10
What formula in sheet 2 A1 will give me what is entered in the table sheet 1 A1:C10
There is usually only one entry made in the table but if you can supply the answer to 1 or 2 entries I would be grateful
=max(A:A)=min(A:A)
FOR TEXT DATA
=COUNTIF(A1:A5,a1)=COUNTIF(A1:A5,"*?")
FOR VALUE DATA
=COUNTIF(A1:A5,A1)=COUNTA(A1:A5)
Both Return TRUE or FALSE
=if({sum(1/countif($A$1:$A$n,A1:An)}=1,"All Same","Not All Same")
I use formula A1=B1 and get value of TRUE / FALSE in C1. I had dragged this formula for 10 rows. Now in cell D2 i tried to put formula..
=if(and(c1="False", c2="true"), "conflict", "no conflict")
but even when the condition is true i am still getting no conflict.
Can you please advice?
thanks,
Manish
@Manish
Remove the " from around True and False
=if(and(c1=False, c2=True), "conflict", "no conflict")
In C1 and C2 you have a Boolean expression and it evaluates as True/False
These are not text, although they do appear as Text, they are not 1/0 although they sometimes behave as 1/0, they are in fact Boolean values True/False
So in your example you can simplify it as
=If( And( Not(C1), C2), "conflict", "no conflict")
=SUMPRODUCT(MATCH(A1:A4,A1:A4,0))=COUNTIF(A1:A4,A1)
Answer to both bonus questions 2 and 3:
=COUNTIF(A1:An,A1)=COUNT(A1:An)
answer to all questions:
={IF(ISERROR(MATCH(FALSE,((A1:An)=$A$1),0)),"same","different")}
this works with numeric, non-numeric, and blanks:
COUNT will not count numeric
COUNTA will count blanks as one
=SUMPRODUCT(1/COUNTIF(B1:J1,B1:J1))
This will tell you how many unique values exist in the selected range. Text or numeric mixed.
{=IF(AND(A1:A9=A2:A10),"EQUAL","NOT EQUAL")}
this is an array formula, insert it with CSE.
COUNTA/UNIQUE
=SUMPRODUCT(A:A)/A1=COUNT(A:A)
=COUNTIF(A1:A4,A1) = COUNTA(A1:A4)