Last week, we had an interesting homework problem – What is the average speed of this road trip?
We received more than 150 answers. But to my surprise, 57 of them are wrong. So today, lets learn how to calculate the average speed correct way.
Please click here to download solution workbook.
What is Speed?
Back in school days, we learned what speed is.
Speed = Distance / Time
Now lets look at the problem
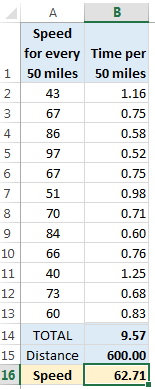
Here is the data:
Jack kept track for every 50 mile interval. And he did that for 12 intervals. So the total distance is 12×50 = 600 miles.
We just need to know how much time Jack took to cover the 600 miles to calculate the speed.
We know that Jack covered first 50 miles @ 43mph.
So the time taken for first 50 miles is 50/43 = 1.16 hrs (or 1 hr & 9 mins)
Like wise, if we calculate times taken for all the 50 miles, we get this:
Isn’t there a way to calculate this without helper column?
Now you are talking.
While the detailed break-up of the calculation above helps us understand how Time, Speed & Distance are related, when answering a question like “What is Jack’s average speed?”, you may want to write a single formula to get the answer (instead of all the extra helper column cells).
The range A2:A13 contains speeds per 50 mile intervals.
The time taken for first 50 mile is =50/A2
The time taken for second 50 mile is = 50/A3
…
So, 50 / (A2:A13) should give us an array of times.
And the total time taken is a simple sum of this array.
So, SUM(50/(A2:A13)) should give the total time.
Now, if we divide 600 by this, we should get our average speed for the entire trip.
Formula #1: Array SUM()
Our first formula for calculating average speed is,
=600 / SUM(50/(A2:A13))
Since this is an array formula, you should press CTRL+Shift+Enter to get it work.
Formula #2: SUMPRODUCT
While the above formula works beautifully, it is a bummer that we must press CTRL+Shift+Enter to get it work. Why not use a formula that can natively process arrays.
Enter SUMPRODUCT.
=600 / SUMPRODUCT(50/(A2:A13))
works just as beautifully and you don’t have to press CSE.
Formula #3: Harmonic Mean
Lets expand the formula and see what is happening, mathematically speaking.
Our formula is,
=600 / SUM ( 50 / (A2:A13) )
in mathematical terms, this is,
= 600 / ? [ 50 / (A2:A13) ]
= 600 / [50/A2 + 50/A3 + 50/A4 + … + 50/A13]
After isolating 50, we get:
= 600 / [50 * (1/A2 + 1/A3 + 1/A4 + … + 1/A13)]
= 12 / (1/A2 + 1/A3 + 1/A4 + … + 1/A13)
Lets call this blue expression as (1).
Time for introducing the concept of Harmonic Mean.
The harmonic mean is the reciprocal of the arithmetic mean of reciprocals.
Sounds confusing?!?
Take a sip of that coffee and read again.
reciprocal of the arithmetic mean of reciprocals
So harmonic mean of a range of numbers (say a,b,c,d…) is
=1/ [(1/a + 1/b + 1/c +…) / (count of numbers)]
or in other words,
= count of numbers / sum of reciprocals
Applying this concept to the range A2:A13, we get
= count of range / sum of reciprocals of A2:A13
= 12 / (1/A2 + 1/A3 + 1/A4 + … + 1/A13)
Now, isn’t the red expression of harmonic mean same as the blue expression (1) above?
Thus, to calculate the average speed, we just need harmonic mean of the the range A2:A13.
And there is a perfect formula for that.
=HARMEAN(A2:A13)
So, we can use that and it gives average speed for the trip in one step!
Special case – What if the speed is not tracked at equal distances?
Lets say Jack measured his speed at 40,50,60,40,60,50,40,50,60,60,50,40 mile intervals instead of every 50 miles.
In such case, we can’t use HARMEAN() because the distances are not equal. Fortunately, we can still use SUMPRODUCT.
Assuming the distance covered per interval is in the range B2:B13 (speeds are already in A2:A13),
The formula,
=SUM(B2:B13)/SUMPRODUCT(B2:B13/A2:A13)
tells us the average speed of the trip.
Learn more: Calculating weighted average using SUMPRODUCT.
Download the solution workbook
Click here to download the solution workbook. Examine the formulas to learn more.
As a bonus, It contains an additional problem to test your skills.
A twist in the tale – Tracking time instead of speed
Lets say after all this formula struggle, Jack (our driver of the road trip) wised up and started tracking time instead of speed. So his new log looks like this:
Now how do we calculate the average speed?
The time stamp data is in range A2:A16 and distance is in B2:B16.
Please post your formulas in the comments section.
PS: The solution workbook contains answer to this problem as well. Just unhide to see.
Go ahead and post your answers. This time, lets hope we get fewer than 1/3rd answers as wrong.
Learn more about formulas:
Check out any article from our formula forensics or Excel homework pages to learn something interesting & cool. Also go thru SUMPRODCUT & Advanced SUMPRODUCT articles to sharpen your formula writing skills.
Listen to our podcasts on averages to raise above your average.
62 Responses to “Introduction to Financial Modeling using Excel [Part 1 of 6]”
Oooh! Chandoo - are you looking to outperform the Altman Z-Score?
I'm all ears 😉
Many thanks, Paramdeep. Looking forward to the remaining parts of the series
Thank you Paramdeep. I look forward to following the series.
Those interested in Financial Modelling may also find this site interesting:
http://www.fimodo.com/
Hi Chandoo,
Really looking forward for this awesome financial modeling journey 🙂
All the very best..
Regards
Rohit1409
Hi Chandoo,
it seems the future is not away when we will have a new software/spreadsheet as competitor to Microsoft Office/Linux etc.......Hats Off to you..
KEEP SMILING
GURU
@apex, clarity: Thanks...
@all: I do hope that you have started creating the model for the simple case given.. Lets see, what according to you all is the best way forward. So your views on the best practices for the template for valuation?
The planning process varies depending on the project and type of data I am looking at.
If I am doing a cost impact study based on actuals, verses a cost impact study to estimate future cost, verses reviewing historical data then creating a model, verse having to review historical data, apply it to a draft model, update the model based on the draft outputs and the presentation then sometimes repeat the process a few times.
Revisions are an absolutely necessary part of corporate financial modeling especially for the presentation sections. A good presentation will be revised multiple time. There are just to many elements which cannot be planned for, especially with ad hoc reports/models.
Revisions are leading cause of errors, and time spent tracking down errors. The more complex the model the more important revision control is. I would be interested in a section on revision control and good methodologies to determine the effect of changes on models. That is without having to due detail review of the whole model over again.
Hi Paramdeep,
I can't wait for the continuation of this series. You have done a great job in making technical terms appear simple and easy to understand. This article is also very useful in our line of business, in fact i will be featuring this article in our site. Of course the credits will go out to you.
Many thanks and keep it up!
Drew
[...] Introduction to Financial Modeling [...]
[...] Introduction to Financial Modeling [...]
[...] Introduction to Financial Modeling [...]
[...] Introduction to Financial Modeling [...]
@Drew: Thanks! Hope that you found the tutorials useful. Feel free to get back with any queries.
[...] you are building financial models or any other type of excel based decision models, chances are, there will be multiple scenarios in [...]
Great information, i also want to learn financial modeling, how to learn
[...] Here is a free financial modeling course to help you get started. Spread some love,It makes you awesome! Tweet [...]
[...] Introduction to Financial Modeling [...]
[...] (if you don’t want to join Financial Modeling School, we are still friends Here is a free tutorial on excel financial modeling.) [...]
chando bhai i m tired for looking financial modeling detail but i cant find it anyway. so plz kindly send me full detail of financial modeling from beginning levelo to final. where i learn complete modeling procedure n order to become professional
You noob, you won`t become a professional like that, you need to do it on your own and learn as you go
@Nadeem Bhai,
The 6 links to the tutorial at the top of this post, build a small integrated financial model step by step. We are also running a complete 8 weeks course on financial modeling (similar to excel school). But that is almost 50% complete right now. If you want to join, you can join the next batch (probably starting in Jan/ Feb)
Feel free to get back, if you have any queries regarding the model/ steps in creating the same
[...] you do not wish to join our course, we are still cool. Here is a 6 part training on financial modeling & 2 part training on project finance. They are free, fresh and [...]
I want to learn how to build a financial model
Dear Lulama,
You can use this tutorial to learn to build a financial model. We also run a course on financial modeling and project finance modeling. The details can be obtained from:
http://chandoo.org/wp/financial-modeling/
You can consider joining that as well.
I would strongly encourage you to join the newsletter to get the updates about financial modeling and the next batch starting for the course.
I want to learn thorough excel and financial modelling thing !!! I am a chartered accountant..CAn you please suggest a detail syllabus that should be learn by me. Also suggest any classes that would cover everything in excel and financial modelling related things.. I stay in mumbai, so please suggest a class in mumbai or any books..byyee.. thanks ..
[...] Financial Modeling using Excel – 6 part tutorial [...]
Hi Vivek,
We do conduct the financial modeling course online as well as in Mumbai. We start with the basics of excel and build a completely integrated financial model in the class. For details you can look at:
http://chandoo.org/wp/financial-modeling/
or
http://www.edupristine.com/courses/financial-modeling/prisitne-fm-offering
Please describe to me various type of financial modela and demonstrate how a model can be build.
Regards,
Dear Immanuel,
This series of articles does exactly that. If you go step by step through the articles and create the excel sheets on your own, you will understand how to create an integrated financial model.
Alternatively, if you are looking for video sessions, you can consider joining our course:
http://chandoo.org/wp/financial-modeling/
It is expected to reopen somewhere in mid july.
[...] Excel Financial Modeling – 6 part tutorial [...]
Thanks Paramdeep this is great!
[...] Few months ago, we learned how to create a project valuation model in Excel as part of our series on Financial Modeling in Excel. [...]
Paramdeep Hi! A bit ignorant here, but let's ask anyway. Can I access "recorded" video sessions apart from following the step by step articles?
Thanks!
@Marius: Yes, we do have a training program with recorded video sessions. If you are interested, you can enroll for the same. The details can be obtained from: http://chandoo.org/wp/financial-modeling/
i want to know about the scope of financial modeling.i also want to know after doing financial modeling course what are the job prospect, like where i can found job so plz send me full detail of financial modeling from beginning levelo to final.
I am interested to join your Financial modelling class cos am involved in a new business. But I have a Macbook Air with Excel for Mac installed. Would that work with your program?
Dear Charsiew,
The complete training program is built using Excel 2007 with MS windows. Though there is nothing specific to Microsoft in the training. I think a few people have joined the program and are using MAC. If you write an email to me on paramdeep @ gmail.com, I can send you the email ids of those participants and you can get to know their feedback and difficulties in using the program.
This is great, when does the next batch start?
Dear Karan,
The course is in recorded format and you can register for the same as soon as you want.
Paramdeep, thanks. I'm venturing into financial modelling for the first time and from the little I've read from your website already, I'm sure I'll find your resources very useful; thanks once again.
Dear Seun,
I am glad that you are finding the resources to be useful. Feel free to send in comments with your feedback and further questions.
hie ppl...I jst wantd a small favour cn smone help me out in calculating EBITDA, along with its working, from wipros annual report 2011-2012, link - http://www.wipro.com/investors/annual-reports.aspx
...PLZ plz... i am having a submission tommorow.
[...] [Related: Introduction to Financial Modeling - 6 part tutorial] [...]
Nice article.
In designing Excel Financial Models I design the user interface as friendly as possible and structuring the input variables in the workflow of the client's operations so that they can flow through the impact of the input variables in Excel using buttons and macros and giving the model transparency.
Cheers
Arthur
[…] 4) http://chandoo.org/wp/2010/07/21/financial-modeling-introduction/ Chandoo has a great 6 step guide which goes through financial modeling from start to finish. Includes loads of pdfs to download including cheat sheets and case studies. Definitely a good place to start learning how to get to grips with financial modeling and Chandoo is well known for its Excel tutorials so if anything doesn’t make sense about the terms used to talk about formatting etc. then the answer can surely be found elsewhere on the website (and often already has hyperlinks added to skip straight to those sections as they are talked about within the financial modeling article!) […]
[…] Financial modeling using Excel (6 part tutorial) […]
Excellent site. Lots of helpful info here.
I am sending it to a few buddies ans also sharing in delicious.
And certainly, thanks in your effort!
[…] Introduction to Excel Financial Modeling […]
Another step to build any financial model is to do a financial analysis beforehand. This normally helps to design and come up with good projections.
Wow great information even I would like to learn financial modeling thanks for sharing this.
Looking For Full details On financial modelling. thank you for sharing this part!
Superb site. Bunches of supportive information here.
I am sending it to a couple of mates and additionally partaking in scrumptious.
Undoubtedly, thanks in your exertion!
Thanks for sharing very useful information
I really appreciate the effort, specially the case study part. This is one piece of information that deserves appreciation.
Nice collection of article, so inspiring and easy to read, keep posting thank you for sharing
Have a Nice Day!
I have to agree with all your inclusions.such a piece of great information that will be very useful for students
I appreciate your effort of writing a value able piece of content.
I really appreciate the effort
This is really awesome, thanks for sharing.
Thanks for the share!
A debt of gratitude is in order for your article! You focused on a point we have just thought to be a couple of times. Our outcome in the past was a "light" adaptation from what you have proposed.
I have to agree with all your inclusions.such a piece of great information that will be very useful for students