“Start with a joke.” My boss used to say when I am nervous about an upcoming presentation. Although, I am not nervous to post this article, I think a joke will always help.
So here it goes:
[originally posted on 5th May 2008]
Now to more serious matters.
VLOOKUP (and other lookup formulas) are very powerful and quite practical. They can fetch you the information you are looking for from a heap of data.
Now that we have seen the power of VLOOKUP thru several posts this week, I want to test your understanding of these formulas by presenting 3 challenges.
Download the excel workbook with these challenges
Click here to download excel workbook with all the data for these challenges.
Challenge # 1: Price After Discount
We come across this problem quite often. You have a list of discount codes and applicable quantity thresholds. For eg. you may sell an item at $50, but if I buy more than 1 item, you will give a 10% discount. The discount goes up as I purchase more quantity.
Now, given a list of item quantities, how do you calculate the amount payable using lookup formulas? That is our first challenge.
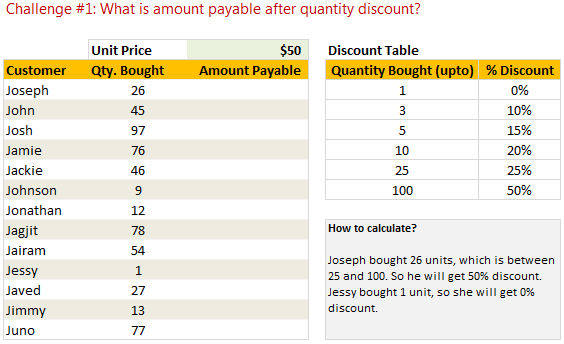
Challenge # 2: Price after accumulated quantity discount
This is essentially same as above formula, but the discounts apply on accumulated quantities bought so far. For eg. I will get first item for 0% discount, 2nd and 3rd items for 10% discount, 4th item for 15% discount … 26th item for 50% discount etc.
Now, given a list of customer names and quantities they bought (in the same order), how do you calculate the amount payable for each transaction?
Challenge # 3: Closest price based on the quantity purchased
This is an interesting challenge. The price after discount is determined based on the quantity bought. For eg. the discount thresholds are 1, 3, 5, 10, 25 etc. Now, given a quantity of items bought, we determine the price by finding the closest threshold to it. So, a quantity of 7 will get the price from threshold 5 as against 10.
Few guidelines on solving these challenges:
Although the above problem might appear simple, the solution is not so straightforward.
- Use a variety of formulas: Do not just rely VLOOKUP. Instead experiment with formulas like SUMIF, COUNTIF, INDEX, MATCH etc. to get results
- Use helper columns: Break down the problem in to several steps and use helper columns to get the results
- Use pen & paper: Write down the logic first, then simulate it in excel using formulas. It clears your mind fast.
- Many solutions exist: Each problem can be solved in several different ways. So once you find a solution, feel free to explore other options
- Share your solutions: Use comments box to share your solutions with us. I am always looking for new ways to solve problems. So teach me…
Solution to the Challenges:
Here is a workbook with one set of solutions for the problems. As I said, many other solutions do exist. So use this workbook as an indication of what is possible.
Click here to download excel workbook with all the data for these challenges.
One Link to More VLOOKUP Awesomeness:
Debra at Contextures has chipped in with some interesting videos on VLOOKUP formulas. Check them out here.
The 2nd Joke:
It is quite difficult to set an expectation and then meet it. More so with jokes. But do you know that Chandoo.org’s 404 pages show Excel error messages? For example go to http://chandoo.org/wp/missing_file/. Refresh the page to see a different message. 🙂
It is Diwali (the festival of lights) in India this weekend. So I am going to spend time with family, light some fireworks and relax. I wish you a happy Diwali if you celebrate one. Even otherwise, I wish a lot of light and warmth in to your life this year.
28 Responses to “CP024: Customize Excel to boost your productivity”
I think that the most useful customisation that I utilise frequently is some code I found that allows multiple items to be selected from a data validation list. For example one workbook we use lists the business drivers for a project. Another uses this technique to select the staff involved in a particular project. See http://blog.contextures.com/archives/2009/09/18/select-multiple-items-from-excel-data-validation-list/
Another terrific podcast Chandoo! Glad to hear that you, your family, friends and community are recovering well from HurHur.
You did a great job of covering so many of the customization techniques that I use but one that I really like is the addition of those top portion of the quick access tool bar with items that I use often but are not standard to any of the tool bar options.
Thank again Chandoo for the terrific website! It definitely is helping to make me awesome in Excel.
I customise excel toolbars by inserting an icon and dragging it to the appropriate area.
I prefer not to customize (too much).. I use Excel on a work pc, on two pc's at home, and sometimes on other PC's (even on different languages). I've found that if I keep the most "standard" look, I manage to get around on any pc, whatever the language pack.
The only thing I do is "pinning" the most used files on the Windows taskbar. And even then I sometimes forget what I placed where, and look it up manually anyway...
Hi, Chandoo. Thanks for the complete review of customizations. I use most of the items you mention, such as Options to set the default font to “old” Arial rather than Cambria. I’ve also adapted the QAT, adding a button to Repeat last action as well as ones to close the current workbook and the Excel application. Lastly, I developed a personal Add-in that contains macros and changes the ribbon (via Microsoft’s Custom UI editor) to rearrange buttons for functions I always use and adds a new ribbon tab with buttons for my personal macros. For example, one of my most frequently used macros deletes all rows below and columns to the right of a selected cell and resets the Excel used range value for the worksheet (helpful for when I press Ctrl-End).
Thank you again for another great podcast! I always learn something from your podcast/Blog/site. I can't believe I never bothered to look at setting the number of sheets excel creates when you open a New workbook. That will save me time everyday!
I usually create a Personal Macro set to use, as well as creating some custom ribbon and toolbar sets to make my most needed functions handy (I even include some personal macros in these toolbars.) I also spend some time creating some themes to match the Company reporting colors so that my work can easily be incorporated into company communications.
Thanks for helping me be awesome at Excel everyday!
Hi Chandoo - excellent podcast. At the moment I only use the quick access tool bar to add not standard icons. But now I have several techniques that I am going to try. Thanks
excellent podcast!! not enough users maximise their productivity by making Excel more comfortable to work with!!
I use many of the techniques already mentioned (personal macro book, customised QAT/ribbon, etc) but but, instead of adding lot's of buttons I find it's better learn and use the relevant keyboard shortcuts instead of adding buttons for all those functions you use all the time (avoid button overload!!).
Far better to add buttons for functions you don't use often and that are difficult to find/use in their regular guise
I also use a default 'dashboard' workbook that has hyperlinks to a handful of files I use regularly.
also maybe worth mentioning creating default workbook/worksheet 'styles' - to do this create a workbook with the formats you want (fonts, page setup, # of sheets, etc) and save it to your excel start folder with the name BOOK (use SHEET for the sheet template). From then on all new books/sheets will have the same basic formatting
Thanks for the podcast Chandoo, glad you are recovering from the typhoon experience.
Here at work we created 2 template files, a "simple" one and a "large" one. We often have to put together engineering calculations and having these templates makes it so much faster. The simple one has a cover page (used for tracking revisions) and then a sheet set out in our standard format. The large one has the same cover page, then a contents page that has macro buttons to jump to any of the 10 tabs set up in it. And yes, we often use 5-10 tabs when doing our calculations! This makes the navigation much easier and means we can get on with calcs and not have to spend time formatting.
Thanks and enjoy, Oxi
Hi Chandoo – I liked this episode. So far I only use quick access bar to add icons for Macros, special paste etc.. Looking forward to explore some of the techniques shared by you. Thanks
Thanks for the podcast. There's a couple of things I'll have to try.
I've set up a default workbook that's saved to my excel start directory that contains:
* corporate colours and fonts
* a cover sheet
* modified and expanded cell styles
* default table and pivot table styles
* custom page setup settings
Another thing I've tried is creating chart templates which saves a bit of time.
My Quick Access toolbar is jampacked with macros:
- Save all open spreadsheets
- Backup the active workbook to another folder. Useful if I'm making big changes to the spreadsheet that i might want to revert later.
- Copy & Paste special values. Why click two buttons when you can click one?
- Set my preferred number formatting
- Format graphs in company colours
- Apply red/green conditional formatting for growths data. 0% growth is white, 20% growth is green, -20% growth is red
- Format and apply settings to pivot tables as I like them. E.g. Tabular format, no retained items, no style, etc
- Sort items in a pivot filter. Standard Excel capability only lets you sort items if they are in rows or columns not in a filter
- Delete all custom styles. It amazing how many junk styles spreadsheets can accrue, especially when copying in data from other spreadsheets
- Resize and reposition all comments. I swear comments have a mind of their own, constantly moving to bizarre places.
- Print in a Userform all external links and whether the links are active. Including those in name manager and in pivot tables that don't show up in the 'Edit links' window.
- Print in a Userform all HIDDEN name manger names. As a company we need to be careful about what is exposed when we publish spreadsheets.
These (and more I've not mentioned) save me countless hours during a normal working week!
Thanks for a great podcast. Really useful tips on customisation. The tip on only one sheet instead of three - using that now myself.
Personally I use customisation for two main purposes. Quick access to functions I use regularly – to state the obvious – but also some functions I use so infrequently I may not be able to quickly find them when I need them. Forms, for example.
And if I ever need to use a function or command that I have recently learned or used in a new or different way, I add that to the Quick Access Ribbon.
Hi Chandoo,
On top all those customization you've mentioned, I also use the Custom UI Editor for Microsoft Office to create my own Ribbon menu buttons in Excel 2007 and hide the default ones. With the help of macros of course, this makes Excel looks and behave like an App.
Try that to impress your boss !
Chandoo,
Until recently, I had only created custom VBA to solve specific problems related to work. I usually placed a shortcut in a new ribbon. Now I am going to use some of the tips that you mentioned to customize one ribbon for all of the common items that I use (like filter, sort, number format, etc.)
Thank you.
Hi Chandoo,
I really like your podcast. I will appreciate if you continue to do podcast in the future.
Regarding my customize of excel, I usually keep lot of commands in Quick Access Toolbars (QAT), esp, insert/delete sheet row, insert/delete sheet column,copy, cut, format copying, paste, paste special, paste value, Font color, Fill color, camera tool and open recent file etc. Also I click on click on Developer tab so that it is visible on my tabs.
When I was studying MBA, I used to do add-ins of Analysis Toolpak but I have not used that Toolpak since I completed MBA.
Thanking you,
Sam
Hi Chandoo,
I really like your page and it's the first time I listen your podcast and it's great!!. I use a lot the Quick Access Toolbar and also use personal macros for rutine task and for look-and-feel in corporate colors, but after listen you I will try to costumize the ribbon and also I will work with themes and styles.
Thanks to inspire us!!.
Regards from Mexico.
Uriel
Thank you Chandoo, very useful.
I have done 3 things to customize my excel,
Created a new tab and put in it all my frequently used commands.
Recorded all my repeated activities as macros and I am running this everyday.
Added the commands I use very very frequently (including the recorded macros) to the QAT.
Thank you again
Hi Chandoo,
Great podcast. I usually do the following to customize my Excel:
1) I use custom themes and chart & slicer templates
2) Custom macros in QAT and Ribbon for repetitive tasks
3) Keep generic VBA routines in a module for use when needed for specific workbooks, I can just copy it into the target workbook.
Thanks,
Dave
Hi Chandoo,
I have been using the quick access toolbar and it is great for having frequently used features all in one place. As well as macros and those less commonly known features, such as select visable cells when working with hidden rows/columns. The list of all commands available to add to the toolbar is mind numbing.
I did not know about adding your own tab to the ribbon. I have already begun contructing my own.
Thank you for the wonderful information.
Chandoo,
I mainly use the personal macros. There are a few charts that I update frequently, this requires that I keep the old data and change the range of the chart. Changing the range causes Excel to pick all new colors for my chart. So, one macro reverses this issue.
Thanks for sharing your awesomeness.
My customization:
I have three add-ins: Macabacus light for shortcuts (free), XL Campus to work with lots of tabs and the Tableau reshaper add-in (free), to reshape tables in database form.
I have created and copied macros for:
Clean formats
Search and select constants
Format as constant (I used to do financial modeling)
Trace dependents simultaneously
Center across selection (not used anymore since it's in one of the Add-ins)
Search and select blanks cells
Select cell A1 in every sheet (before closing the file)
Protect and unprotect sheets and workbook
Almost all macros have shortcuts and a dedicated tab in the ribbon.
As for Excel options themselves:
Automatic calculations
Error tracking disabled
Cursor stays in same cell when Enter is pressed
And I used to have a Financial modeling template as a predefined sheet where different formats and styles were pre-established
Dear chandoo
Thanks for the excellent podcast. I regularly visit your website and have listened to all your podcast which are very informative. I customise my toolbar by using a quick access and inserting icons in toolbar.
i used all of you suggestions, but have refrained from pinning files to the Recent Workbook List. It bothered me that this pinned files also took over the keybord shortcuts for the last opened files. If I press ALT-F+1, i want to open the last used file, not the file i pinned first.
I missed a very powerful Excel customization option in your podcast, which i use every day and saves me hours: custom keyboard shortcuts. There are two of them:
1. Assign a Key combination to a macro (e.g. "Ctrl-Shift-V" for my VBA-procedure "PasteSpecial_Values")
-> Open the Macro-dialog (Alt-F8) and go to Options, set the key...
2. Assign a Key combination even to F-Keys (e.g. "F5" for "my_favorite_Macro")
-> Open VBA-Editor (Alt-F11), go to any Module in your Personal.xlsb and add this code:
Sub auto_open()
Application.OnKey "{F5}", "my_favorite_Macro"
End Sub
There is no quicker way to call your macro!
Hi Chandoo, very excellent podcast.
I use the quick access toolbar to link my VBA macro's and at the moment I'm experimenting on adding a personal ribbon tab with personal ribbon buttons. I use a Custom UI Editor to do this, it let me link macro's to the buttons used in the personal ribbontab.
This way for a project dashboard I can add the buttons necessary there and they are attached to the file. So other people opening the file have the same ribbon tab. Looking professional and to quote 'awesome' ;-).
Thanks for your prodcast.
I customize my excel in the ribbon. This allows to feature the items I need
Hi Chandoo,
Would you please link me to your Excel Customization Handbook? I am sure that this will help me in a huge way!
Hi Chandoo!
I would love an Excel Customization Handbook! Here is my tip:
To recreate the CTRL-HOME functionality on Excel for Mac copy and paste the following code into your personal macro workbook. I assigned my code to the hotkey Option-Cmd-G and now it's like I have a "Home" button on my Mac!
----------
Sub GoHome()
'
' GoHome Macro
' Simulates Ctrl-Home on a PC
'
' Keyboard Shortcut: Option+Cmd+g
If ActiveSheet.Type = xlWorksheet Then
With ActiveWindow
.ScrollRow = 1
.ScrollColumn = 1
.ActivePane.VisibleRange.Cells(1).Select
End With
End If
End Sub