In early February Sujit asked a question at Chandoo.org, original post.
I require a formula stating criteria [0%-25% output will be 0, 26%-50% output will be 0.1, 51%-75% output will be 0.2, 76%-100% output will be 0.3 & 100% + output will be 0.4]
Kyle, responded with a neat Sumproduct formula
=SUMPRODUCT((B3>{0.25,0.5,0.75,1})*0.1)
I think it is so neat that it is worthy of sharing and detailing here at Formula Forensics:
So today we will pull Kyle’s answer apart to see what’s inside.
Kyle’s Formula
As usual we will work through this formula using a sample file for you to follow along. Download Here.
Kyle’s formula is a Sumproduct based formula
=SUMPRODUCT((B3>{0.25,0.5,0.75,1})*0.1)
Lets look at cell C3 as our example.
;
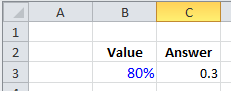In C3 we see the formula: =SUMPRODUCT((B3>{0.25,0.5,0.75,1})*0.1)
Which consists of a Sumproduct function and a formula inside the sumproduct.
We know from Formula Forensics 007 that Sumproduct, Sums the Product of the Arrays, and that when there is only 1 array it simply sums the array elements.
In this case the Sumproduct only has a single array as an element
=SUMPRODUCT((B3>{0.25,0.5,0.75,1})*0.1)
and so the (B3>{0.25,0.5,0.75,1})*0.1 component must return an Array of elements for the Sumproduct to sum.
If we now look at the (B3>{0.25,0.5,0.75,1})*0.1 component.
We can see that it consists of a comparison B3>{0.25,0.5,0.75,1}
The result of the comparison is Multiplied by 0.1.
Sujit’s orginal question asked: 0%-25% output will be 0, 26%-50% output will be 0.1, 51%-75% output will be 0.2, 76%-100% output will be 0.3 & 100% + output will be 0.4
And Kyles formula is using B3>{0.25,0.5,0.75,1} to work out which category the value in B3 belongs to.
We can see this if in a blank cell say C5: we enter the following:
= B3>{0.25,0.5,0.75,1} press F9 not Enter.
Excel will respond with ={TRUE,TRUE,TRUE,FALSE}
This is showing us that the 1st, 2nd and 3rd elements in the formula: B3>{0.25,0.5,0.75,1}, are True
In our example the value in B3 is 80% which is 0.8 which is Greater than 0.25 and Greater than 0.5 and Greater than 0.75, but Not Greater than 1.0.
The next part of Kyle’s formula is (B3>{0.25,0.5,0.75,1})*0.1
In a blank cell say C7: enter the following:
= B3>{0.25,0.5,0.75,1}*0.1 press F9 not Enter.
Excel will respond with ={0.1,0.1,0.1,0}
This is showing us the result of
=(B3>{0.25,0.5,0.75,1})*0.1
={TRUE,TRUE,TRUE,FALSE} *0.1
={0.1,0.1,0.1,0}
Sumproduct now only has to add up the Array
=Sumproduct({0.1,0.1,0.1,0})
Which it does returning 0.3.
The Neat Part
The neat part of this is that Kyle has used the 0.1 Multiplier to Force the array to an array of Numbers for Sumproduct to sum.
Had Kyle used: =SUMPRODUCT((B3>{0.25,0.5,0.75,1}))*0.1
Excel would have returned an answer of 0
This is because as we saw in Formula Forensics 007, Sumproduct doesn’t know what to do with the array of True/False, they need to be converted to numerical equivalents for Sumproduct to operate on.
In a spare cell, say C9, enter: =SUMPRODUCT((B9>{0.25,0.5,0.75,1}))*0.1
Excel will respond with 0
Of course that can be fixed by using a double degative of a 1* inside the formula
In a spare cell, say C10, enter either:
=SUMPRODUCT(1*(B9>{0.25,0.5,0.75,1}))*0.1
or
=SUMPRODUCT(- -(B9>{0.25,0.5,0.75,1}))*0.1
Excel will respond with 0.3 as it should
Except that the formula is longer and now has to do 1 more multiplication.
Download
You can download a copy of the above file and follow along, Download Here.
Formula Forensics “The Series”
You can learn more about how to pull Excel Formulas apart in the following posts
We Need Your Help
I have received a few more ideas since last week and these will feature in coming weeks.
I do need more ideas though and so I need your help.
If you have a neat formula that you would like to share and explain, try putting pen to paper and draft up a Post like above or;
If you have a formula that you would like explained but don’t want to write a post also send it to Chandoo or Hui.
13 Responses to “Gantt Box Chart Tutorial & Template – Download and Try today”
Hi Chandoo
As one of your students I have followed your detailed example through with great success. However, Excel is acting in an unexpected way and I wonder if you could take a look?
http://cid-95d070c79aef808e.office.live.com/self.aspx/.Public/Gantt%20Box%20Chart.xlsm
On my version, I have to type 40239 (Which equates to 2 Mar 2010) to get the chart to display 31 May 2010 (which should be 40329)!!??
Have I done something wrong or is Excel acting up?
Thx
Oli
PS Your example file in 2007 displays correctly.
Hi,
I like this idea a lot, but I agree the name is a little drab.
As an American I may just be seeing things, but to me the combination of lines and bars on your chart looks like a bunch of cricket bats.
Maybe you could work that into a catchier name. 🙂
Cheers!
Here is some code I use to keep the axis synched.
It may be useful to some of your readers
It is based on a comment I saw on Daily Dose of Excel.
Function SynchGanttAxis(Cname, lower, upper)
'Sets the X min and X max for Category axis
Application.Volatile
On Error Resume Next
'
'Top Horizontal Axis
With ActiveSheet.Shapes(Cname).Chart.Axes(xlCategory, 1)
.MinimumScale = lower
.MaximumScale = upper
End With
'Bottom Horizontal Axis
With ActiveSheet.Shapes(Cname).Chart.Axes(xlValue, 2)
.MinimumScale = lower
.MaximumScale = upper
End With
End Function
Function SynchVerticalAxis(Cname, lower, upper)
Application.Volatile
On Error Resume Next
' Excel 2007 only
'Right hand vertical axis
With ActiveSheet.Shapes(Cname).Chart.Axes(xlValue, 1)
.MinimumScale = 0
.MaximumScale = upper
End With
End Function
@Oli.. Can you check your file again.. I see 40329...
@Dave: Even I saw things.. the bars actually looked like lollipops. How about calling this lollipop chart - now that would be yummy and goes along the tradition of naming charts after eatables (bar, pie, donut...)
@Bob: Superb stuff... thanks for sharing 🙂
Hi Chandoo
This looks really good and I think it can also be applied to show project phases / milestones.
Question: Thinking further could this be amended to display a project lifecycle (Idea through to Implementation say 7 phases) on one bar / row? Just imagine 20 projects within a programme all on one chart one bar each showing their respective lifecycle stages i.e. on one page.
Idea: As the Gantt Box Chart this is quite intensive to set up re formatting etc how about the added extra of once you have completed this to "Save as template" i.e. saves the formatting and layout of the chart as a template so you can apply to future charts. Simple to do and will save the time formatting etc again and again and again.
Therefore tip: Click on your chart demo and then click on Save As template icon (2007) - edit file name and click on save. Ready to use / apply via Templates in Change Chart Type window.
Thanks and be very interested if the lifecycle question can be resolved
Mike
How embarrassing.
I was obviously suffering from numerical dyslexia. I was one of those days.
@Mike H: You can easily make this chart to work like a generic project lifecycle plan chart. All you have to do is,
1. in a separate sheet define the steps of lifecycle and various dates in a table (with 5 columns for each of the projects you have).
2. now use a control cell to input the project name you want to show in the chart
3. based on the input, use OFFSET Formulas to get the correct data
4. Rest is same as the tutorial above
For more info on the dynamic charting visit http://chandoo.org/wp/tag/dynamic-charts/ and http://chandoo.org/wp?s=OFFSET
Your solution is really smart but in the en Excel isn't meant to do stuff like this. I, as a former PM, always thought is was frustrating that you had to do stuff like this for something simple like a Gantt chart. So I built Tom's Planner. And would like to plug it here. I think it really solves the problem you are trying to solve in the most efficient way. Check out http://www.tomsplanner.com for a free account or play around with the demo.
Hi there,
Chandoo - this is really a very nice and helpfull chart - I adopted it, so I can report a forecast or the delay of a certain task (coming from my role as an auditor for projects).
One topic I´m currently struggeling with: I do have a project lasting for lets say 12 month. For a management reporting, I want to have kind of snapshot, lets say one month back and 2 month in the future. I tried with the offset formula, but failed. Any idea?
Thx
Lopi
[...] Ein viel geliebter Klassiker ist die Erstellung von GANTT-Diagrammen mit Excel. Wir hatten das Thema wiederholt schon hier. Chandoo.org hat sich mal wieder mit einer neuen Variante hervorgetan: Das GANTT-Box-Chart. [...]
[...] [...]
Hi Chandoo - fantastic xls. One thing I can't figure out how to do is adjust the alignment of the vertical axis. I would like to left align so that I could indent to represent sub tasks. Can that be done? Or is there a better way?
I've been trying to work out if there's a way to show weekends on the graph. The closest thing I've got is to add them on a secondary axis, but then I haven't been able to keep both axis lined up together! Any ideas?
Following on from this - is it possible to show things like holidays?