You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
sum of Maximum value from range of unique data set
- Thread starter xlstime
- Start date
NARAYANK991
Excel Ninja
xlstime
Active Member
Thanks Luke, I have highlighted the values based on customer name, you can check the logic in the attachment. basically I need sum of maximum values against each customer and need only one value
What's the logic for the numbers you highlighted? Why 20 and not the 21 or 24? If instead it should be the largest 4 numbers, you could do this formula:
=SUM(LARGE(B2:B10,{1,2,3,4}))
xlstime
Active Member
Thanks Narayank, can you please help with without helper column.
Hi ,
See if this works.
Narayan
xlstime
Active Member
Thanks Nebu, really appreciate your efforts, but i need this thru formula only
Thanks
Thanks
Chihiro
Excel Ninja
Another way to do it (helper column but at result table).
D14: Confirmed as array (CSE)
=INDEX($A$2:$A$10,MATCH(0,COUNTIF($D$13:D13,$A$2:$A$10),0))
E14: Excel 2016
=MAXIFS($B$2:$B$10,$A$2:$A$10,D14)
F14: Excel 2013 or older, confirmed as array (CSE)
=MAX(IF($A$2:$A$10=D14,$B$2:$B$10,0))
Edit: If there should not be any helper column... you'd need to hard code condition.
D14: Confirmed as array (CSE)
=INDEX($A$2:$A$10,MATCH(0,COUNTIF($D$13:D13,$A$2:$A$10),0))
E14: Excel 2016
=MAXIFS($B$2:$B$10,$A$2:$A$10,D14)
F14: Excel 2013 or older, confirmed as array (CSE)
=MAX(IF($A$2:$A$10=D14,$B$2:$B$10,0))
Edit: If there should not be any helper column... you'd need to hard code condition.
Attachments
NARAYANK991
Excel Ninja
Hi ,
What does the following array formula , entered using CTRL SHIFT ENTER , do ?
=SUM((COUNTIFS(A2:A10,A2:A10,B2:B10,">=" & B2:B10) = 1) * (B2:B10))
Narayan
What does the following array formula , entered using CTRL SHIFT ENTER , do ?
=SUM((COUNTIFS(A2:A10,A2:A10,B2:B10,">=" & B2:B10) = 1) * (B2:B10))
Narayan
@Narayan - nice idea. It works ok in this case but what if there is more than one entry equal to the maximum value? (eg if 15 is changed to 20 in the fourth line then that proposal will not include Smith )
Perhaps an alternative that only counts any maximum once is:
=SUM(IF(FREQUENCY(MATCH(A2:A10,A2:A10,0)-1,MATCH(A2:A10,A2;A10,0)-1/RANK(B2:B10,B2:B10)),B2:B10))
Perhaps an alternative that only counts any maximum once is:
=SUM(IF(FREQUENCY(MATCH(A2:A10,A2:A10,0)-1,MATCH(A2:A10,A2;A10,0)-1/RANK(B2:B10,B2:B10)),B2:B10))
Chihiro
Excel Ninja
Just for fun. Method using MS Query.
1. Create new query from Get External Data-> From Other Sources
2. Choose New Data Source, name the data source and select type of database as "Microsoft Excel Driver [*.xls, ...., *.xlsb]
3. Connect to your file (as long as it was saved beforehand it can be the same workbook you are working in)
4. Move over columns you want into right pane and cancel out and hit OK to edit in Query Editor
5. Hit "SQL" button and edit query. It will be like below in this case.
6. Load the result to anywhere on the sheet as table.
Note: Some distinct disadvantages
1. You need to keep filename consistent
2. If location of the file changes. SQL need to be edited either manually or through VBA to keep it dynamic.
1. Create new query from Get External Data-> From Other Sources
2. Choose New Data Source, name the data source and select type of database as "Microsoft Excel Driver [*.xls, ...., *.xlsb]
3. Connect to your file (as long as it was saved beforehand it can be the same workbook you are working in)
4. Move over columns you want into right pane and cancel out and hit OK to edit in Query Editor
5. Hit "SQL" button and edit query. It will be like below in this case.
Code:
Select SUM([maxSale]) As [sumMaxSale]
From (
SELECT Distinct `Sheet1$`.Customer,
Max(`Sheet1$`.Sales) As [maxSale]
FROM `C:\YourFilePath\sampleQuery.xlsb`.`Sheet1$` `Sheet1$`
Group by `Sheet1$`.Customer
)6. Load the result to anywhere on the sheet as table.
Note: Some distinct disadvantages
1. You need to keep filename consistent
2. If location of the file changes. SQL need to be edited either manually or through VBA to keep it dynamic.
xlstime
Active Member
Narayan,
Can you please help me to understand this formula
Can you please help me to understand this formula
n tHi ,
What does the following array formula , entered using CTRL SHIFT ENTER , do ?
=SUM((COUNTIFS(A2:A10,A2:A10,B2:B10,">=" & B2:B10) = 1) * (B2:B10))
Narayan
xlstime
Active Member
Lori,
Can you please help me to understand this formula
Can you please help me to understand this formula
@Narayan - nice idea. It works ok in this case but what if there is more than one entry equal to the maximum value? (eg if 15 is changed to 20 in the fourth line then that proposal will not include Smith )
Perhaps an alternative that only counts any maximum once is:
=SUM(IF(FREQUENCY(MATCH(A2:A10,A2:A10,0)-1,MATCH(A2:A10,A2;A10,0)-1/RANK(B2:B10,B2:B10)),B2:B10))
NARAYANK991
Excel Ninja
Hi ,
I'll explain Lori's formula , as that is the one which you should be using , since it will work in every situation.
The formula , which is :
=SUM(IF(FREQUENCY(MATCH(A2:A10,A2:A10,0)-1,MATCH(A2:A10,A2;A10,0)-1/RANK(B2:B10,B2:B10)),B2:B10))
makes use of 5 functions ; out of these , the use of SUM and IF needs no explanation. The remaining 3 can be explained as follows :
1. What does the MATCH function do , when the first parameter is not a single value , but a range of values ?
It returns an array of values.
The segment :
MATCH(A2:A10,A2:A10,0)
will return an array as follows :
{1;2;3;1;1;2;7;2;3}
What this means is that the first 3 values are unique , to be found in the first , second and third cells in the range i.e. in cells A2 , A3 and A4.
The fifth and sixth values are the same as the first value ; the seventh value is the same as the second value , and so on.
Subtracting 1 from this returns the array :
{0;1;2;0;0;1;6;1;2}
----------------------------------------------------------------------------------
2. What does the FREQUENCY function do ? Using the following construct :
FREQUENCY(MATCH(A2:A10,A2:A10,0) , MATCH(A2:A10,A2:A10,0))
or even
FREQUENCY(MATCH(A2:A10,A2:A10,0) - 1 , MATCH(A2:A10,A2:A10,0) - 1)
would have returned the following array :
{3;3;2;0;0;0;1;0;0;0}
What this tells us is that the first value in the range A2:A10 occurs 3 times , the second value occurs 3 times , the third value occurs 2 times , while the seventh value ( Johnson ) occurs only once.
The FREQUENCY function returns a value against the first occurrence of an item , and returns zeroes for other occurrences of that item. Thus , against the first occurrence of Smith there is a 3 , while against the second and third occurrence of Smith , there are zeroes.
So far , there is nothing which gives us an indication of how this can ever help us towards a solution. Now comes the surprising twist - the use of the RANK function !
The RANK function ranks the values of the Sales from 1 through 9 , with 1 being assigned to the maximum sales value , and 9 being assigned to the minimum sales value.
Now what happens when we use this along with the MATCH function as the second parameter to the FREQUENCY function ?
Instead of returning the array of values
{0;1;2;0;0;1;6;1;2}
we have an array of values
{0.8;1.5;2.88888888888889;0.857142857142857;0.833333333333333;1.75;6.875;1.66666666666667;2}
Let us see what happens when the FREQUENCY function is used with the above 2 arrays.
Suppose we take the first name Smith ; there are 3 occurrences of the same name , in the first , fourth and fifth cells of the range.
The sales values corresponding to these 3 occurrences of Smith are 20 , 15 and 16.
The RANK function gives these occurrences ranks of 5 , 7 and 6.
By using this as the divisor , 1/RANK will result in a higher value corresponding to the rank of 5 than 6 and 7. Since we are subtracting this result , the higher value being subtracted will give us a lower value corresponding to a rank of 5 compared to the ranks of 6 and 7.
Hence , the three values corresponding to Smith , instead of being 0 , 0 , 0 , are now 0.8 , 0.857 and 0.833
Assigning the value of 0 from the first parameter into the bins will naturally assign it to 0.8
The lowest value of 0.8 now corresponds to the maximum sales of 20.
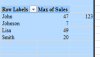
Similarly , if we consider John , there are 3 occurrences of the same name , in the second , sixth and eighth cells of the range.
The sales values corresponding to these 3 occurrences of John are 47 , 21 and 24.
The RANK function gives these occurrences ranks of 2 , 4 and 3.
By using this as the divisor , 1/RANK will result in a higher value corresponding to the rank of 2 than 4 and 3. Since we are subtracting this result , the higher value being subtracted will give us a lower value corresponding to a rank of 2 compared to the ranks of 4 and 3.
Hence , the three values corresponding to John , instead of being 1 , 1 , 1 , are now 1.5 , 1.75 and 1.66
Assigning the value of 1 from the first parameter into the bins will naturally assign it to 1.5
The lowest value of 1.5 now corresponds to the maximum sales of 47.
Thus , using the 3 functions MATCH , RANK and FREQUENCY ensures that the result will have non-zero values in those places corresponding to the maximum sales figures for each person ; the IF function now retrieves those values , while the SUM function is the final piece of the puzzle.
Narayan
I'll explain Lori's formula , as that is the one which you should be using , since it will work in every situation.
The formula , which is :
=SUM(IF(FREQUENCY(MATCH(A2:A10,A2:A10,0)-1,MATCH(A2:A10,A2;A10,0)-1/RANK(B2:B10,B2:B10)),B2:B10))
makes use of 5 functions ; out of these , the use of SUM and IF needs no explanation. The remaining 3 can be explained as follows :
1. What does the MATCH function do , when the first parameter is not a single value , but a range of values ?
It returns an array of values.
The segment :
MATCH(A2:A10,A2:A10,0)
will return an array as follows :
{1;2;3;1;1;2;7;2;3}
What this means is that the first 3 values are unique , to be found in the first , second and third cells in the range i.e. in cells A2 , A3 and A4.
The fifth and sixth values are the same as the first value ; the seventh value is the same as the second value , and so on.
Subtracting 1 from this returns the array :
{0;1;2;0;0;1;6;1;2}
----------------------------------------------------------------------------------
2. What does the FREQUENCY function do ? Using the following construct :
FREQUENCY(MATCH(A2:A10,A2:A10,0) , MATCH(A2:A10,A2:A10,0))
or even
FREQUENCY(MATCH(A2:A10,A2:A10,0) - 1 , MATCH(A2:A10,A2:A10,0) - 1)
would have returned the following array :
{3;3;2;0;0;0;1;0;0;0}
What this tells us is that the first value in the range A2:A10 occurs 3 times , the second value occurs 3 times , the third value occurs 2 times , while the seventh value ( Johnson ) occurs only once.
The FREQUENCY function returns a value against the first occurrence of an item , and returns zeroes for other occurrences of that item. Thus , against the first occurrence of Smith there is a 3 , while against the second and third occurrence of Smith , there are zeroes.
So far , there is nothing which gives us an indication of how this can ever help us towards a solution. Now comes the surprising twist - the use of the RANK function !
The RANK function ranks the values of the Sales from 1 through 9 , with 1 being assigned to the maximum sales value , and 9 being assigned to the minimum sales value.
Now what happens when we use this along with the MATCH function as the second parameter to the FREQUENCY function ?
Instead of returning the array of values
{0;1;2;0;0;1;6;1;2}
we have an array of values
{0.8;1.5;2.88888888888889;0.857142857142857;0.833333333333333;1.75;6.875;1.66666666666667;2}
Let us see what happens when the FREQUENCY function is used with the above 2 arrays.
Suppose we take the first name Smith ; there are 3 occurrences of the same name , in the first , fourth and fifth cells of the range.
The sales values corresponding to these 3 occurrences of Smith are 20 , 15 and 16.
The RANK function gives these occurrences ranks of 5 , 7 and 6.
By using this as the divisor , 1/RANK will result in a higher value corresponding to the rank of 5 than 6 and 7. Since we are subtracting this result , the higher value being subtracted will give us a lower value corresponding to a rank of 5 compared to the ranks of 6 and 7.
Hence , the three values corresponding to Smith , instead of being 0 , 0 , 0 , are now 0.8 , 0.857 and 0.833
Assigning the value of 0 from the first parameter into the bins will naturally assign it to 0.8
The lowest value of 0.8 now corresponds to the maximum sales of 20.
Similarly , if we consider John , there are 3 occurrences of the same name , in the second , sixth and eighth cells of the range.
The sales values corresponding to these 3 occurrences of John are 47 , 21 and 24.
The RANK function gives these occurrences ranks of 2 , 4 and 3.
By using this as the divisor , 1/RANK will result in a higher value corresponding to the rank of 2 than 4 and 3. Since we are subtracting this result , the higher value being subtracted will give us a lower value corresponding to a rank of 2 compared to the ranks of 4 and 3.
Hence , the three values corresponding to John , instead of being 1 , 1 , 1 , are now 1.5 , 1.75 and 1.66
Assigning the value of 1 from the first parameter into the bins will naturally assign it to 1.5
The lowest value of 1.5 now corresponds to the maximum sales of 47.
Thus , using the 3 functions MATCH , RANK and FREQUENCY ensures that the result will have non-zero values in those places corresponding to the maximum sales figures for each person ; the IF function now retrieves those values , while the SUM function is the final piece of the puzzle.
Narayan